Распознанный текст из DJVU-файла, 25 — страница
злб 3.80. Бесконечно большая пласти- на нз однородного диэлектрика с проиицаемостью е заряжена равномерно сторонним зарядом с объемной плотностью р. Толщина пластины равна Ы. Найти: а) модуль вектора напряженности электрического поля и потенциал как функции расстояния 1 от середины пластины (потенциал в середине пластины положить равным нулю); взяв координатную ось х перпендикулярно к пластине, изобразить примерные графики зависимостей проекции Е (х) вектора Е и потенциала ф (х); б) поверхностную и объемную плотности связанного заряда. 3,81. Сторонние заряды равномерно распределены с объемной плотностью р ) О по шару радиуса Я из однородного изотропного диэлектрика с проницаемостью з. Найти: а) модуль вектора напряженности электрического поля как функцию расстояния г от центра шара; изобразить примерные графики зависимостей Е (г) и
р (г); б) объемную и поверхностную плотности связанных зарядов. 3.82. Круглый диэлектрический диск радиуса Я и толшины д поляризован статически так, что поляризованность, равная Р, всюду одинакова и вектор Р лежит в плоскости диска.
Найти напряженность Е электрического поля в центре диска, если Й . 20 21 22 23 24 25 26 27 28 29 . 77
Обкладками сферического конденсатора являются две концентрические сферы (R1 и R2). Сообщим этим поверхностям одинаковые по величине, но разноимённые заряды +q и –q и вычислим электрическое поле, создаваемое этими зарядами в пространстве (рис. 2.10.).
Сферы делят пространство на 3 области:

Выберем замкнутую гауссову поверхность внутри первой области. Разумно, руководствуясь соображениями симметрии, эту поверхность выбрать сферической (r1).
Поток вектора напряжённости через эту поверхность (по определению потока) равен:

Этот поток, согласно теореме Гаусса, пропорционален заряду, заключённому внутри поверхности. Но внутри сферы радиуса r1 заряд отсутствует. Поэтому и поток равен нулю
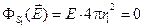 (!)
(!)
Отсюда заключаем, что в области I поле равно нулю
0 R2). Вычисляем поток вектора напряжённости

Этот поток равен нулю, так как он пропорционален алгебраической сумме зарядов, заключённых внутри этой поверхности. Но алгебраическая сумма одинаковых разноимённых зарядов равна нулю
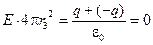
График Е = Е(r) приведён на рисунке 2.11.

Лекция 3 «Потенциал электростатического поля»
3.1. Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
3.2. Теорема о циркуляции вектора напряжённости электростатического поля.
3.3. Связь напряжённости и потенциала электростатического поля.
3.4. Примеры расчёта потенциала электростатического поля.
3.4.1. Потенциал поля точечного заряда.
3.4.2. Разность потенциалов на обкладках сферического конденсатора.
Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика.
Потенциал — энергетическая характеристика поля, связанная и с энергией заряда в электростатическом поле и с работой, совершаемой электрической силой при перемещении заряда.
Дата добавления: 2014-01-04 ; Просмотров: 1531 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет


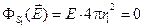 (!)
(!)