Предел бесконечность на бесконечность в степени бесконечность

С непосредственным вычислением пределов основных элементарных функций разобрались.

При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.

Перечислим все основные виды неопределенностей: ноль делить на ноль 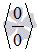( 0 на 0 ), бесконечность делить на бесконечность 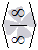, ноль умножить на бесконечность 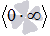, бесконечность минус бесконечность 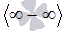, единица в степени бесконечность 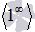, ноль в степени ноль 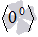, бесконечность в степени ноль .

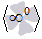ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.

Раскрывать неопределенности позволяет:

• упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
• использование замечательных пределов;
• применение правила Лопиталя;
• использование замены бесконечно малого выражения ему эквивалентным (использование таблицы эквивалентных бесконечно малых).

Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).

Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.

Приведем парочку примеров, когда все сразу получается после подстановки значения и неопределенности не возникают.

Вычислить предел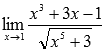

Подставляем значение:

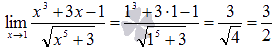
И сразу получили ответ.

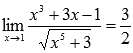
Вычислить предел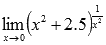

Подставляем значение х=0 в основание нашей показательно степенной функции:

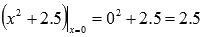
То есть, предел можно переписать в виде

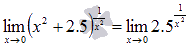
Теперь займемся показателем. Это есть степенная функция 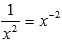. Обратимся к таблице пределов для степенных функций с отрицательным показателем. Оттуда имеем 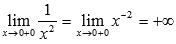и 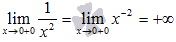, следовательно, можно записать .

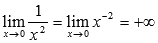Исходя из этого, наш предел запишется в виде:

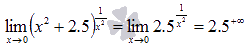
Вновь обращаемся к таблице пределов, но уже для показательных функций с основанием большим единицы, откуда имеем:

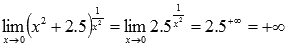
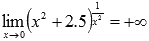
Разберем на примерах с подробными решениями раскрытие неопределенностей преобразованием выражений.

Очень часто выражение под знаком предела нужно немного преобразовать, чтобы избавиться от неопределенностей.

Вычислить предел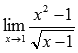

Подставляем значение:

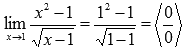
Пришли к неопределенности. Смотрим в таблицу неопределенностей для выбора метода решения. Пробуем упростить выражение.

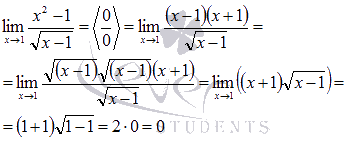
После преобразования неопределенность раскрылась.

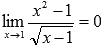
Вычислить предел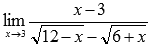

Подставляем значение:

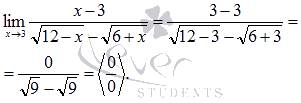
Пришли к неопределенности ( 0 на 0 ). Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Домножим и числитель и знаменатель на выражение, сопряженное знаменателю.

Для знаменателя сопряженным выражением будет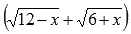

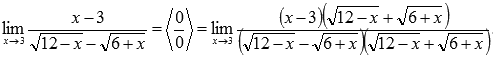
Знаменатель мы домножали для того, чтобы можно было применить формулу сокращенного умножения – разность квадратов и затем сократить полученное выражение.

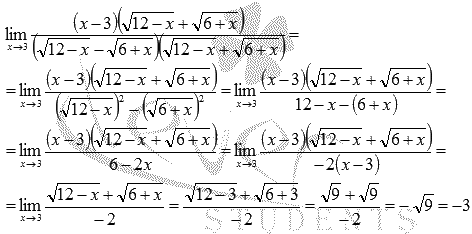
После ряда преобразований неопределенность исчезла.

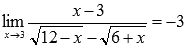
ЗАМЕЧАНИЕ: для пределов подобного вида способ домножения на сопряженные выражения является типичным, так что смело пользуйтесь.

Вычислить предел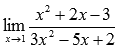

Подставляем значение:

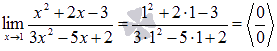
Пришли к неопределенности. Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Так как и числитель и знаменатель обращаются в ноль при х=1 , то если разложить на множители эти выражения, можно будет сократить (х-1) и неопределенность исчезнет.

Разложим числитель на множители:

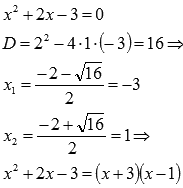
Разложим знаменатель на множители:

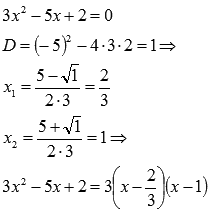
Наш предел примет вид:

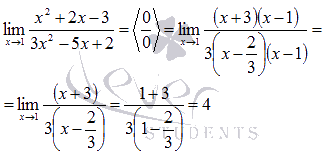
После преобразования неопределенность раскрылась.

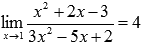
Рассмотрим пределы на бесконечности от степенных выражений. Если показатели степенного выражения положительны, то предел на бесконечности бесконечен. Причем основное значение имеет наибольшая степень, остальные можно отбрасывать.

Пример.

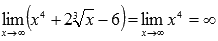
Пример.

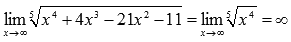
Если выражение под знаком предела представляет собой дробь, причем и числитель и знаменатель есть степенные выражения ( m – степень числителя, а n – степень знаменателя), то при 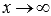возникает неопределенность вида бесконечность на бесконечность 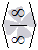, в этом случае неопределенность раскрывается делением и числитель и знаменатель на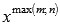

Вычислить предел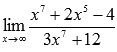

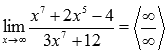
Степень числителя равна семи, то есть m=7 . Степень знаменателя также равна семи n=7 . Разделим и числитель и знаменатель на .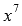

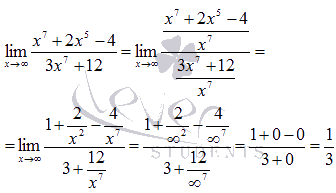
Рассмотрим основные типы неопределенностей пределов на бесконечности с примерами решений:

1. $ [frac<0><0>] $
2. $ [infty — infty] $
3. $[frac<infty><infty>]^ <[infty]>и [1 ^ infty] $

Пример 1

Вычислить предел функции, стремящейся к бесконечности $ lim _limits frac$

Решение

Первым делом подставляем $ x o infty $ в предел, чтобы попытаться его вычислить.
$$ lim _limits frac = frac<infty> <infty>= $$

Вычисление не дало результата, так как появилась неопределенность. Чтобы устранить её, вынесем за скобки в числителе и знаменателе $x$ с наибольшей степенью.

Максимальная степень у $x^3$, поэтому вынесли именно её, а затем выполнили сокращение. Пользуясь тем, что $lim_limits frac<1> = 0$ получаем ответ.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ $$ lim _limits frac = 1 $$

Так как предел стремится к бесконечности, то подставляем её в функцию под знаком предела.

Получили неопределенность. Для избавления от неё умножим и разделим функцию под знаком предела на сопряженную к ней. Она будет отличаться только одним знаком.

По формуле разности квадратов $ (a-b)(a+b) = a^2-b^2 $ сворачиваем числитель. А знаменатель пока не трогаем.

Снова подставляем бесконечность в предел и получаем $frac<1><infty>$, что равняется нулю. Поэтому записываем сразу ответ.

Пример 2

Решить предел с бесконечностью $lim_limits sqrt-x$

Решение

Ответ

$$ lim_limits sqrt-x = 0 $$

При подставлении $x o infty $ в предел получаем неопределенность. $$ lim_limits igg (frac<3x-4> <3x+2>igg)^frac <2>= igg[frac<infty><infty>igg]^ <[infty]>$$

Для решения примера понадобится формула второго замечательного предела. $$lim_limits igg(1+frac<1> igg)^x = e qquad (1) $$

Из выражения, стоящего под знаком предела вычитаем единицу, чтобы его подстроить под формулу (1).

Перепишем предел из условия задачи в новом виде и подставим в него $x o infty$.

Пользуясь формулой (1) проведем вычисление лимита. В скобках перевернем дробь.

По условиями формулы второго замечательного предела (1) в скобках знаменатель дроби должен быть равен степени за скобкой. Выполним преобразование степени. Для этого умножим и разделим на $frac<3x+2><-6>$.

Остаётся сократить степень экспоненты и найти её предел.

Предел дроби равен отношению коэффициентов при старшей степени $x$.

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

(Здесь 0 <displaystyle 0> — бесконечно малая величина, а ∞ <displaystyle infty > — бесконечно большая величина)

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов ( 0 0 ) <displaystyle left(

0^<0>
ight)> , ( 1 ∞ ) <displaystyle left(1^<infty >
ight)> , ( ∞ 0 ) <displaystyle left(infty ^<0>
ight)> пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

0^<0>
ight)=left(e^<0cdot ln <0>>
ight)=left(e^<0cdot (-infty )>
ight)> ( 1 ∞ ) = ( e ∞ ⋅ ln ⁡ 1 ) = ( e ∞ ⋅ 0 ) <displaystyle left(

1^<infty >
ight)=left(e^<infty cdot ln <1>>
ight)=left(e^<infty cdot 0>
ight)> ( ∞ 0 ) = ( e 0 ⋅ ln ⁡ ∞ ) = ( e 0 ⋅ ∞ ) <displaystyle left(

infty ^<0>
ight)=left(e^<0cdot ln <infty >>
ight)=left(e^<0cdot infty >
ight)>

Для раскрытия неопределённостей типа ∞ ∞ <displaystyle <frac <infty ><infty >>> используется следующий алгоритм:

1. Выявление старшей степени переменной;
2. Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа ( 0 0 ) <displaystyle left(<frac <0><0>>
ight)> существует следующий алгоритм:

1. Разложение на множители числителя и знаменателя;
2. Сокращение дроби.

Для раскрытия неопределённостей типа ( ∞ − ∞ ) <displaystyle (infty -infty )> иногда удобно применить следующее преобразование:

Пусть f ( x ) → x → a ∞ <displaystyle f(x)<xrightarrow >infty > и g ( x ) → x → a ∞ <displaystyle g(x)<xrightarrow >infty > ; lim x → a [ f ( x ) − g ( x ) ] = ( ∞ − ∞ ) = lim x → a ( 1 1 f ( x ) − 1 1 g ( x ) ) = lim x → a 1 g ( x ) − 1 f ( x ) 1 g ( x ) ⋅ 1 f ( x ) = ( 0 0 ) <displaystyle lim _[f(x)-g(x)]=(infty -infty )=lim _left(<frac <1><frac <1>>>-<frac <1><frac <1>>>
ight)=lim _<frac <<frac <1>>-<frac <1>>><<frac <1>>cdot <frac <1>>>>=left(<frac <0><0>>
ight)> .

Данный вид неопределённостей может раскрываться с использованием асимптотических разложений уменьшаемого и вычитаемого, при этом бесконечно большие члены одного порядка должны уничтожаться.

При раскрытии неопределённостей также применяются замечательные пределы и их следствия.

Пример [ править | править код ]

0>"> lim x → a a x − x a x − a , a > 0 <displaystyle lim _<frac -x^>>,a>0> 0>"/> — пример [1] неопределённости вида ( 0 0 ) <displaystyle left(<frac <0><0>>
ight)> . По правилу Лопиталя lim x → a a x − x a x − a = lim x → a a x ln ⁡ a − a x a − 1 1 = a a ( ln ⁡ a − 1 ) <displaystyle lim _<frac -x^>>=lim _<frac ln a-ax^><1>>=a^(ln a-1)> . Второй способ — прибавить и отнять в числителе a a <displaystyle a^> и дважды применить теорему Лагранжа, к функциям a x <displaystyle a^> и x a <displaystyle x^> соответственно:

a x − x a x − a = a x − a a − ( x a − a a ) x − a = a c ln ⁡ a ( x − a ) − a d a − 1 ( x − a ) x − a = a c ln ⁡ a − a d a − 1 <displaystyle <frac -x^>>=<frac -a^-(x^-a^)>>=<frac ln a(x-a)-ad^(x-a)>>=a^ln a-ad^>

здесь c, d лежат между a и x, поэтому они стремятся к a при x стремящемся к a, отсюда получаем тот же предел, что и в первом способе.

Пример 3

Решить предел на бесконечности $lim_limits igg (frac<3x-4> <3x+2>igg)^frac <2>$

Решение