Содержание
Пусть дана формула А, подлежащая преобразованию в КНФ. Если А — это пропозициональный символ /?, либо его отрицание -н/?, то ее КНФ состоит из единственного дизъюнкта, каковым является самор, либо р. Если же это не так, то надлежит выполнить следующие действия.
1. Исключение из Л связок -> и =, используя теоремы:
2. Внесение связки -> внутрь скобок везде, где это возможно, применяя законы де Моргана: 
В результате этих действий связка будет расставлена в формуле А только перед пропозициональными символами или перед их отрицаниями. Вследствие этого могут появиться выражения вида —•—./?.
3. Удаление двойных отрицаний в соответствии с законом двойного отрицания 
4. Применение закона дистрибутивности
необходимое число раз, пока не будет получена КНФ.
Для получения ДНФ этим же алгоритмом нужно на этапе 4 применять второй из законов дистрибутивности
необходимое число раз, пока не будет получена ДНФ.
Пример. Приведем к КНФ следующую формулу:
1. Исключение импликаций
2. Внесение связки внутрь скобок
3. Удаление двойных отрицаний
4. Применение закона дистрибутивности (av(bAC)) v ((avb)A(avc)) 
Следовательно, исходная формула эквивалентна КНФ D]aD2 aD3, где
Приведение к ДНФ той же формулы выполняется точно также, и видно, что уже на этапе 3 искомая ДНФ построена, т. е. исходная формула эквивалентна ДНФ C1vC2vC3vC4, где 
Конъюнктивная нормальная форма играет важную роль в обработке знаний на ЭВМ: дизъюнкты, входящие в КНФ, являются посылками в принципе резолюции, используемом в качестве единственного правила вывода в механизме вывода языков логического программирования. Например, синтаксической основой языка программирования PROLOG являются предложения Хорна, а его логической основой является принцип резолюции.
Что умеет калькулятор математической логики?
- Расставлять скобки в выражении, учитывая приоритет операций
- Упрощать логические выражения
- Строит таблицу истинности для введённых формул
- Найти нормальные формы логического выражения:
- Конъюнктивную нормальную форму (КНФ), в том числе совершенную
- Дизъюнктивную нормальную форму (ДНФ), в том числе совершенную
Поддерживаемые символы в логических выражениях
Здесь указаны символы, которые стоит указывать при вводе логической формулы в калькулятор.
¬a — отрицание a⇒b — импликация a∧b — конъюкция a∨b — дизъюнкция a⇔b — эквиваленция a⊕b — сложение по модулю 2 (Исключающее или) a|b — Не-и (штрих Шеффера) a↓b — Не-или (стрелка Пирса)
Это символы не жёстко привязаны к соотв. операциям, можно использовать другие.
Примеры логических выражений
С применением отрицания
Со знаком "эквивалентно"
Со знаком "следствие"
С применением конъюкции и дизъюнкции
С применением Не-и и Не-или
В калькуляторе вы сможете упростить выражения, содержащие следующие операции: NOT, XOR, AND, OR, NAND, NOR, NOT
© Контрольная работа РУ — калькуляторы онлайн
Например,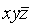 
является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение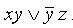 
является ДНФ.
Например, выражение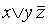 
является ДНФ, но не СДНФ. Выражение 
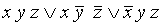является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение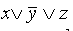 
– простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение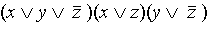 
– КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение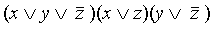 
является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
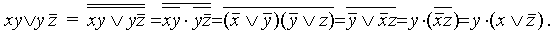
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
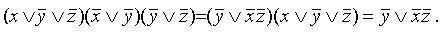
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые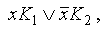 
, то ко всей дизъюнкции добавляем слагаемое К1К2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,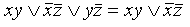 
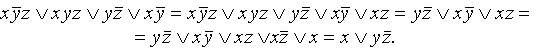
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ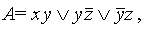 
, после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
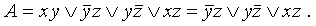
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение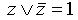 
,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
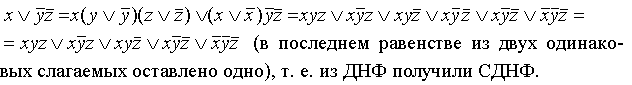
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение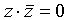 
(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
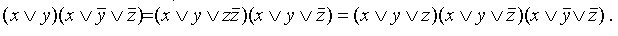
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Загрузка...
