2.3.1. Определение.
Пусть даны линейные уравнения:
a1x + b1y + c1z = d1, (2.3.1)
a2x + b2y + c2z = d2, (2.3.2)
a3x + b3y + c3z = d3. (2.3.3)
Если требуется найти общее решение уравнений (2.3.1) ¾ (2.3.3), то говорят, что они образуют систему. Система, состоящая из уравнений (2.3.1) ¾ (2.3.3), обозначается следующим образом:
 (2.3.4)
(2.3.4)
Общее решение уравнений, составляющих систему, называется решением системы. Решить систему (2.3.4) ¾ это значит либо найти множество всех его решений, либо доказать, что их нет.
Как и в предыдущих случаях, ниже мы найдем условия, при которых система (2.3.4) имеет единственное решение, имеет более одного решения и не имеет ни одного решения.
2.3.2. Определение. Пусть дана система (2.3.4) линейных уравнений. Матрицы
 и
и 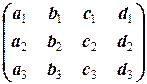
называются соответственно (основной) матрицей и расширенной матрицей системы.
2.3.3. Определения равносильных систем вида (2.3.4), а также элементарных преобразований 1-го и 2-го типов вводятся аналогично, как и для систем из двух уравнений с двумя и тремя неизвестными.
Элементарным преобразованием 3-го типа системы (2.3.4) называется перемена местами некоторых двух уравнений этой системы. Аналогично предыдущим случаям систем из 2-х уравнений при элементарных преобразованиях системы получается система, равносильная данной.
2.3.4. Упражнение. Решить системы уравнений:
а)  б)
б) 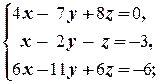 в)
в) 
г) 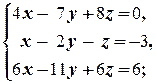 д)
д)  е)
е) 
ж) 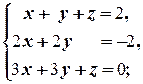 з)
з) 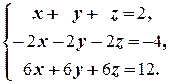
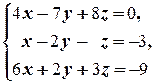
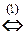
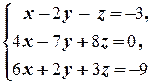

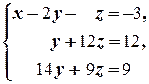
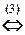
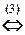
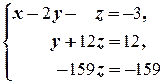
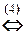
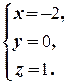
(1) Поменяли местами первое и второе уравнения системы (преобразование 3-го типа).
(2) Первое уравнение, умноженное на 4, вычли из второго, и первое уравнение, умноженное на 6, вычли из третьего (преобразование 2-го типа); таким образом, из второго и третьего уравнений исключили неизвестную x.
(3) Второе уравнение, умноженное на 14, вычли из третьего; из третьего исключили неизвестную y.
(4) Из последнего уравнения находим z = 1, подставляя которое во второе, находим y = 0. Наконец, подставляя y = 0 и z = 1 в первое уравнение, находим x = -2.ñ
б) 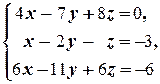
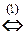
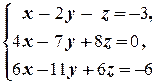


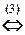
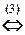
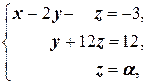
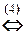
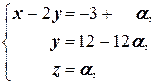

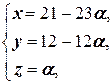
(1) Поменяли местами первое и второе уравнения системы.
(2) Первое уравнение, умноженное на 4, вычли из второго, и первое уравнение, умноженное на 6, вычли из третьего.
(3) Второе и третье уравнения совпали. Одно из них исключаем из системы (или, по-другому, если вычесть из третьего уравнения второе, то третье уравнение обратится в тождество 0 = 0;оно исключается из системы. Полагаем z = a.
(4) Подставляем z = a во второе и первое уравнения.
(5) Подставляя y = 12 — 12a в первое уравнение, находим x.
в) Если первое уравнение разделить на 4, а третье ¾ на 6, то придём к равносильной системе
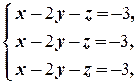
которая равносильна уравнению x — 2y — z = -3. Решения этого уравнения известны (см. Пример 2.2.3 б))
г) 
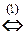
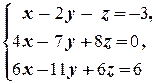

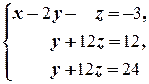
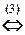
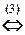
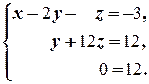
Последнее равенство в полученной системе является противоречивым. Следовательно, система решений не имеет.
Преобразования (1) и (2) ¾ точно такие же, как и соответствующие преобразования системы б))
(3) Из последнего уравнения вычли второе.
б) (21 — 23a; 12 — 12a; a), aÎR;
в) <(-3 + 2a + b; a; b)|a, bÎR>;
г) Система решений не имеет.
2.3.5. Из предыдущих примеров вытекает, что система с тремя неизвестными, как и система с двумя неизвестными, может иметь единственное решение, бесконечное множество решений и не иметь ни одного решения. Ниже мы разберём все возможные случаи. Но предварительно введём некоторые обозначения.
Через D обозначим определитель матрицы системы:
D=  .
.
Через D1 обозначим определитель, полученный из D заменой первого столбца на столбец свободных членов:
D1= 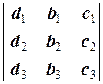 .
.
D2= 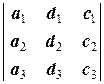 и D3=
и D3=  .
.
2.3.6. Теорема. Если D¹0, то система (2.3.4) имеет единственное решение
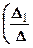 ,
, 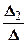 ,
, 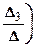 . (2.3.5)
. (2.3.5)
Формулы (2.3.5) называются формулами Крамера.
3.3.7. Упражнение. Решить системы по формулам Крамера.
а)  б)
б)  в)
в) 
Следующая теорема ¾ о множестве решений системы (2.3.4) для случая, когда D=0.
2.3.8. Теорема. Пусть дана система (2.3.4), D ¾ определитель системы и D=0. Тогда:
1) Если хотя бы один из определителей D1, D2 или D3 не равен нулю, то система решений не имеет.
2) Если хотя бы один из определителей 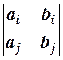 ,
, 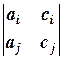 или
или 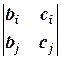 (i¹j) не равен нулю и D1 = D2 = D3 = 0, то система имеет бесконечное множество решений, зависящих от одного параметра.
(i¹j) не равен нулю и D1 = D2 = D3 = 0, то система имеет бесконечное множество решений, зависящих от одного параметра.
3) Если 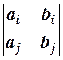 =
= 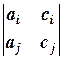 =
= 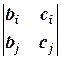 = 0 для всех i¹j и хотя бы один из определителей
= 0 для всех i¹j и хотя бы один из определителей  ,
,  ,
, 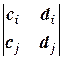 не равен нулю, то система решений не имеет.
не равен нулю, то система решений не имеет.
4) Если 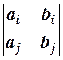 =
= 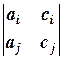 =
= 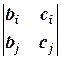 =
=  =
=  =
= 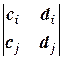 = 0 для всех i¹j, то система имеет бесконечное множество решений, зависящих от двух параметров.
= 0 для всех i¹j, то система имеет бесконечное множество решений, зависящих от двух параметров.
2.3.9. Упражнение. Исследовать системы упражнения 2.3.4 на наличие решений и решить их.
Не нашли то, что искали? Воспользуйтесь поиском:
62. Одно уравнение с тремя неизвестными . Пусть имеем уравнение
На это уравнение можно смотреть, как на запись задачи: найти числовые значения для x, y и z, чтобы трехчлен 3x + 4y – 2z оказался равен числу 11. Таким образом это уравнение является уравнением с тремя неизвестными. Так как мы можем решить одно уравнение с одним неизвестным, то уже с первого взгляда возникает мысль, что 2 неизвестных здесь являются как бы лишними, и им можно давать произвольные значения. И действительно, если, например, взять для y число 3 и для z число 5, то получим уравнение с одним неизвестным:
Возьмем другие числа для y и z. Например, пусть
Тогда получим уравнение:
Продолжая эту работу дальше, мы придем к заключению:
Одно уравнение с тремя неизвестными имеет бесконечно много решений, и для получения их надо двум неизвестным давать произвольные значения.
Результаты этой работы можно записать в таблице (мы, кроме двух уже найденных решений, записали в ней еще одно, которое получится, если положить y = –1 и z = –2):
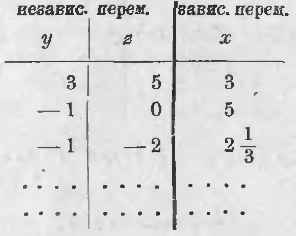
Так как для y и для z мы берем произвольные значения, то они являются независимыми переменными, а x является зависимым (от них) переменным. Другими словами: x является функциею от y и z.
Чтобы удобнее получать решения этого уравнения, можно определить из него x через y и z. Получим:
3x + 4y – 2z = 11; 3x = 11 – 4y + 2z;
x = (11 – 4y + 2z) / 3.
Дадим, напр., значения: y = 5 и z = 1; получим: x = (11 – 20 + 2) / 3 = –2(1/3) и т. д.
Возьмем еще уравнение
Примем x и y за независимые переменные, а z — за зависимое и определим z через x и y
–2z = 7 – 3x + 5y; 2z = 3x – 5y – 7; z = (3x – 5y – 7) / 2
После того, как автор сайта смог научить своего бота решать линейное диофантово уравнение с двумя переменными, возникло желание научить бота решать подобные уравнения, но уже с тремя неизвестными. Пришлось окунутся в книги.
Вынырнув оттуда через два месяца, автор понял, что он ничего не понял. Зело умные математики, так мудрёно писали алгоритм вывода формул, что мне смертному было стыдно. Опечалился было, но мысль на книжных просторах все таки одну полезную нашел, и с этой мысли пришло понимание как решать диофантовые уравнения с тремя неизвестными.
Итак для всех, кто не математик, но хочет им быть 🙂
Диофантовое уравнение с тремя неизвестными имеет вот такой вид
где целые числа
Если мы подумаем какое же общее решение может быть у неизвестных, то самое банальное выглядит так
Подставим наше общее решение в уравнение
Какой же от этого прок, спросит нетерпеливый читатель? А вот какой, сгруппируем все по неизвестным,получим
Смотрите, в правой части стоит какое то постоянное число, обозначенное буквой d
Значит, от t ( она же переменная, мало ли каким она значением хочет стать) оно не зависит а значит
Логично предположить что и от z оно не зависит а значит
а вот от постоянных значений A3 и B3 оно зависит напрямую , то есть
Что же в конечном итоге мы получили? А получили мы три типовых классических диофантовых уравнений с двумя неизвестными, которые решать мы можем легко и непринужденно.
В первых строках поисковых систем нашлось вот такое уравнение
Первое уравнение будет вот такое
Избавимся от нулей, взяв к примеру k=-1. ( Хотите можете взять 2 или 100 или -3) На окончательное решение это не повлияет.
Решаем второе уравнение
здесь пусть k=0 ( так как X и Y не совпадают уже при нулевых значениях)
И последнее третье уравнение
Корни тут такие
Подставим теперь все найденные значения в общий вид
Заметьте, что все решается очень легко и прозрачно! Наверняка преподаватели и способные студенты возьмут себе на вооружение эту методику, так как в книгах автор бота её так и нашел.
Еще один пример, уже решенный с помощью бота.
| Результат решения диофантового уравнения с тремя неизвестными |
| Целочисленные корни такого уравнения следующие |
Дополнение: Когда будете решать подобные уравнения с помощью бота, можете столкнуться с тем, что бот Вам выдаст ошибку с просьбой, поменять переменные местами, для другой попытки решить уравнение. Это связано с тем что при промежуточных вычислениях, получается нерешаемое уравнение
При попытке решить уравнение
мы получим ошибку, так как при любых значениях, в левой части будет всегда(!!) чётное число, а в правой части как мы видим нечетное.
Но это не значит что изначальное уравнение нерешаемое. Достаточно поменять слагаемые в другом порядке, например так
и получаем ответ
| Целочисленные корни такого уравнения следующие |
Дополнение от 23 ноября 2015 года
Зашел спор как решать уравнение подобное этому
Мол, позволяет ли методика которая была описана выше определить существует ли целочисленные решения этому уравнению?
Я не могу доказать, но предполагаю, что если при всех циклических перестановках слагаемых как это было показано на примере уравнения у нас получаются нерешаемые линейные уравнения, то такое уравнение нерешаемое.
В нашем примере так и получается что при любых переставновках, в левой части линейного уравнения всегда(!) будут НЕ взаимно простые числа, и НОД их не является делителем числа в правой части уравнения ( =8 )
Таким образом утверждается что такое диофантовое уравнение нерешаемое в целых числах, но зато оно решается в случае рациональных дробей
при любых значениях z и t уравнение будет верным
По горячим следам, окончательное дополнение от 23 нобяря 2015
Все таки я ошибся в последнем примере. решаемое оно
Так что вышеописанная методика и бот, применим ТОЛЬКО для тех случаев, когда хотя бы одна пара слагаемых из левой части являются взаимно простыми числами.
Если конечно не воспользуетесь новым калькулятором который лишен, всех этих недостатков


