Прямоугольник отличный от квадрата

Вопрос по геометрии:

Начертите квадрат и примите его за единицу измерения площадей. Далее начертите: а) квадрат, площадь которого выражается числом 4; б) прямоугольник, отличный от квадрата, площадь которого выражена числом 4; в) треугольник, площадь которого выражается числом 2. Ребята срочно пожалуйста)) Даю 45 баллов

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

«Будущие исследователи – будущее науки» 19.01.2013

7.1. Найдите два натуральных числа т и п, если известно, что и тп = 2013.

Решение следует из разложения на простые множители и небольшого перебора делителей числа 2013; всего их 8, причем «кандидатом» на роль числа m являются меньшие делители, а именно четыре числа 1, 3, 11, 33 и из них условию удовлетворяет только m=33 при п = 61.

7.2. Найдите сумму всех трехзначных натуральных чисел, в записи которых нет ни цифры 0, ни цифры 5.

Ответ: 284160. Решение. Будем складывать числа столбиком. Каждая последняя цифра встречается в разряде единиц столько раз, сколько есть трехзначных чисел с этой цифрой на конце. Значит, она встретится раза (т. к. всего используется 8 цифр для разрядов сотен и десятков). Поэтому сумма цифр в последнем разряде равна = 2560. Аналогично, в разряде десятков и сотен получим ту же сумму. В итоге получим .

7.3. Дан прямоугольник, отличный от квадрата. Известно, что площадь прямоугольника численно равна его периметру. Докажите, что меньшая сторона прямоугольника меньше 4, а большая сторона – больше 4.

Решение. Пусть – стороны прямоугольника. По условию, , отсюда получаем равенство . Если и , то , что противоречит полученному равенству. Аналогичное противоречие получается, когда оба числа а – 2 и b – 2 положительны, но меньше 2. Если оба числа а – 2 и b – 2 отрицательны, то , что также невозможно. Значит, , , т. е. a 4.

7.4. На острове живут рыцари и лжецы. Рыцари всегда говорят правду, лжецы всегда лгут (островитяне знают, кто есть кто). Турист, прибывший на остров, встретил компанию островитян из 10 человек и стал спрашивать по очереди каждого: "Кого в вашей компании больше: рыцарей, лжецов или, может быть, поровну"? Пятеро сказали одно и то же: "Лжецов больше". Что сказали остальные пять человек?

Ответ: "Поровну". Решение. Предположим сначала, что в компании больше пяти лжецов. Тогда первые пятеро сказали правду, и значит, они рыцари. Итак, рыцарей по меньшей мере пять, и, значит, наше предположение неверно. Предположим теперь, что в компании больше пяти рыцарей. Тогда среди первой пятерки должен оказаться рыцарь, и он должен был сказать правду, а на самом деле он сказал, что больше лжецов, т. е. опять приходим к противоречию. Значит, в компании 5 лжецов и 5 рыцарей. Поскольку первые пятеро сказали неправду, то они лжецы, а остальные – рыцари, и они сказали: "Поровну".

8.1. Стозначное натуральное число N составлено из единиц и двоек, причем между любыми двумя двойками находится четное количество цифр. Известно, что N делится на 3. Сколько единиц и сколько двоек в записи числа N?

Ответ: две двойки и 98 единиц. Решение. Если в записи числа N больше двух двоек, то рассмотрев любые три двойки, получим противоречие: действительно, между первой и второй двойкой – четное количество цифр, между второй и третьей – четное количество, а вместе с самой второй (т. е. средней) двойкой получится нечетное количество. С другой стороны, в записи числа N должны присутствовать хотя бы две двойки, т. к. иначе сумма цифр равнялась бы 100 (если двоек нет) или 101 (если одна двойка), и. N не делилось бы на 3. В случае двух двоек все условия выполнены, когда между ними четное количество единиц.

8.2. Найдите сумму всех трехзначных натуральных чисел, в записи которых нет ни цифры 0, ни цифры 5.

Ответ: 284160. См. задачу 7.2.

8.3. На острове живут рыцари и лжецы. Рыцари всегда говорят правду, лжецы всегда лгут (островитяне знают, кто есть кто). Турист, прибывший на остров, встретил компанию островитян из 10 человек и стал спрашивать по очереди каждого: "Кого в вашей компании больше: рыцарей, лжецов или, может быть, поровну"? Пятеро сказали одно и то же: "Лжецов больше". Что сказали остальные пять человек?

Ответ: "Поровну". См. задачу 7.4.

8.4. В треугольнике АВС биссектриса АМ перпендикулярна медиане ВК. Найдите отношения ВP:PK и AP:PM, где P – точка пересечения биссектрисы и медианы.

Ответ: ВP:PK = 1, AP:PM = 3:1. Решение. Треугольники АВР и АКР равны (сторона АР – общая, и прилегающие к ней углы равны по условию). Значит, АВ = АК = КС, ВР = РК. Поэтому треугольники АВМ и АКМ равны (по двум сторонам и углу между ними). Тогда SABM = SAKM = SCKM = =, где S = SABC. Далее, . Но (т. к. ), . Отсюда , , т. е. и поэтому АР: РМ = 1: 3.

9.1. Стозначное натуральное число N составлено из единиц и двоек, причем между любыми двумя двойками находится четное количество цифр. Известно, что N делится на 3. Сколько единиц и сколько двоек в записи числа N?

Ответ: две двойки и 98 единиц. См. задачу 8.1.

9.2. Числа х, у удовлетворяют системе уравнений

.

Какое наибольшее и какое наименьшее значение может принимать произведение ху ?

Ответ: Наибольшее значение равно 1/3, наименьшее равно –1.

Решение. Имеем = = , т. е. . Система равносильна исходной (т. к. из нее с помощью указанных выше преобразований получается второе уравнение исходной системы). Решение полученной системы – это корни квадратного уравнения (по обратной теореме Виета). Дискриминант этого уравнения должен быть неотрицательным, т. е. . Поэтому .

9.3. Сколько точек на гиперболе имеют целочисленные координаты (х;у)?

Ответ: 16. Решение. Целочисленные точки в первом квадранте соответствуют натуральным делителям числа . Количество таких делителей равно 8 (можно их выписать непосредственно или воспользоваться формулой для количества натуральных делителей числа .) С учетом симметричных точек в третьем квадранте получаем ответ.

9.4. В треугольнике АВС биссектриса АМ перпендикулярна медиане ВК. Найдите отношения ВP:PK и AP:PM , где P – точка пересечения биссектрисы и медианы.

10.1. Числа х, у удовлетворяют системе уравнений

.

Какое наибольшее и какое наименьшее значение может принимать произведение ху ?

Ответ: Наибольшее значение равно 1/3, наименьшее равно –1. См. задачу 9.2.

10.2. Сколько точек на гиперболе имеют целочисленные координаты (х;у)?

10.3. Существует ли такое число х, для которого оба числа и являются рациональными?

Ответ: Не существует. Решение. Предположим, от противного, что , , где p и q — рациональные числа. Тогда = . Если , то отсюда сразу получаем противоречие (в левой части – рациональное число, в правой – иррациональное). Если , то , что также приводит к противоречию, т. к. , а .

10.4. Дан прямоугольник, для которого численное значение площади больше периметра. Докажите, что периметр прямоугольника больше 16.

Решение. Пусть a, b – стороны прямоугольника. Из условия задачи (*)

Сначала проверим, что оба множителя (a – 2) и (b – 2) положительны. Действительно, в противном случае из (*) следует, что a –2 8 P > 16.

11.1. Решите уравнение .

Ответ: , .

Решение. Поскольку , то равенство может выполняться лишь при условии , откуда следует ответ.

11.2. Изобразите на координатной плоскости множество точек, удовлетворяющих неравенству .

Решение. При x > 0 исходное неравенство запишется в виде , т. е. множество из правой полуплоскости лежит между графиками у = х и у = х2 + х. Легко проверить, что парабола у = х2 + х касается прямой у = х в начале координат (см. рис.). При x

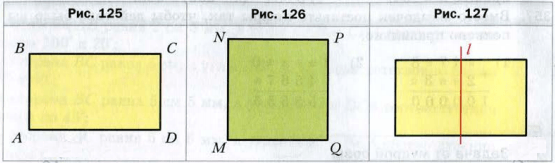
Если в четырехугольнике все углы прямые, то его называют прямоугольником.

На рисунке 125 изображен прямоугольник ABCD.

Стороны AB и BC имеют общую вершину B. Их называют соседними сторонами прямоугольника ABCD. Также соседними являются, например, стороны BC и CD.

Соседние стороны прямоугольника называют его длиной и шириной.

Стороны AB и CD не имеют общих вершин. Их называют противоположными сторонами прямоугольника ABCD. Также противолежащими являются стороны BC и AD.

Противолежащие стороны прямоугольника равны.

На рисунке 125 AB = CD, BC = AD. Если длина прямоугольника равна a, а ширина − b, то его периметр вычисляют по уже знакомой тебе формуле:

P = 2 a + 2 b

Прямоугольник, у которого все стороны равны, называют квадратом (рис. 126 ).

Проведем прямую l, проходящую через середины двух противолежащих сторон прямоугольника (рис. 127 ). Если лист бумаги перегнуть по прямой l, то две части прямоугольника, лежащие по разные стороны от прямой l, совпадут.

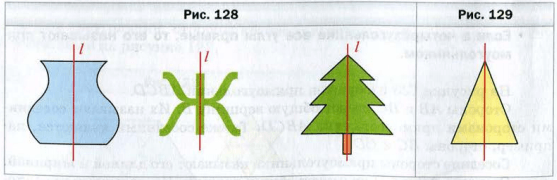
Аналогичным свойством обладают фигуры, изображенные на рисунке 128 . Такие фигуры называют симметричными относительно прямой . Прямую l называют осью симметрии фигуры .

Итак, прямоугольник − это фигура, имеющая ось симметрии. Также ось симметрии имеет равнобедренный треугольник (рис. 129 ).

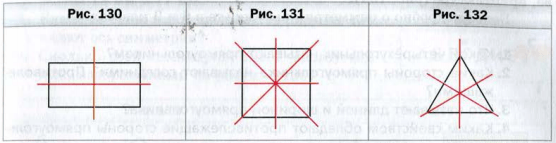
Фигура может иметь более одной оси симметрии. Например, прямоугольник, отличный от квадрата, имеет две оси симметрии (рис. 130 ), а квадрат − четыре оси симметрии (рис. 131 ). Равносторонний треугольник имеет три оси симметрии (рис. 132 ).

Изучая окружающий мир, мы часто встречаемся с симметрией. Примеры симметрии в природе показаны на рисунке 133 .

Объекты, имеющие ось симметрии, легко воспринимаются и приятные для глаза. Недаром в Древней Греции слово "симметрия" служило синонимом слов "гармония", "красота".

Идея симметрии широко используется в изобразительном искусстве, архитектуре (рис. 134 ).