Учитывая, что здесь находится прямоугольник длиной l и шириной b , задача состоит в том, чтобы найти область самого большого эллипса, который может быть вписан в него.
Примеры:
Рекомендуется: Пожалуйста, сначала попробуйте подход , прежде чем переходить к решению.
Подход :
- Пусть длина большой оси эллипса = 2x и длина малой оси эллипса = 2y
- Из диаграммы видно, что
2x = 1
2y = b - Итак, Площадь эллипса = (π * x * y) = (π * l * b) / 4
Ниже приведена реализация вышеуказанного подхода:
Процедуру построения эллипса из окружности путем сжатия можно выполнить с помощью циркуля и линейки следующим образом. Проводим две концентрические окружности радиуса OA=a и OВ=b. Через центр О проводим произвольный луч ОР. Через точки К и N, в которых OР встречает две окружности, проводим прямые, параллельные осям Х и Y. Эти прямые пересекутся в точке M. Ее ордината MQ меньше ординаты NQ точки N, лежащей на окружности радиуса а, причем MQ:NQ=b:a. Значит, точка M лежит на искомом эллипсе. Меняя направление луча ОР, получим новые точки эллипса (рис. 4). На рисунке 5 показано, как построить овал, похожий на эллипс с полуосями а и b (когда а и b отличаются друг от друга не слишком сильно), из дуг окружностей двух радиусов. Для этого надо на отрезке АВ от точки В отложить отрезок длины a-b, поставить точку Е и провести перпендикуляр через середину отрезка АЕ до пересечения с прямой BD. Точку пересечения с прямой BD назовем О1, точку пересечения с прямой АС назовем О2. Из этих точек, как из центров, проведем две сопрягающиеся дуги, радиусами О1В и О2А, соответственно. Центры О3 и О4 симметричны центрам О1 и О2. Если на том же чертеже построить опорные точки для эллипса методом сжатия окружности, будет видно, насколько сильно различаются линии овала и эллипса.
Из уравнения эллипса можно заключить, что оси координат являются осями симметрии эллипса. Центр симметрии О называется центромэллипса. Эллипс можно вписать в прямоугольник, который называется характеристическим(рис. 6). Длины сторон прямоугольника ищутся из простых соображений. Из уравнения эллипса следует, что 
. Аналогично, 
. Следовательно, длины сторон характеристического прямоугольника равны 2a и 2b, соответственно. Числа а и b — называются полуосямиэллипса. Большая полуось называется главной. Из точки В1 проведем дугу окружности радиуса а, точки пересечения этой дуги с осью симметрии эллипса А1А2 назовем F1 и F2. Это фокусыэллипса. Расстояние между ними обозначим через 2c. Ось симметрии, на которой расположены фокусы, называется фокальной осью, а величина с (расстояние от центра эллипса до фокуса) – фокусное расстояние эллипса.Фокусное расстояние эллипса – очень важная характеристика. Эллипс можно задавать и с помощью величины его главной полуоси и фокусного расстояния. Величины a b и c, являясь катетами и гипотенузой прямоугольного треугольника, связаны друг с другом простыми соотношениями (рис. 6):
Сумма расстояний от вершины В1 эллипса до фокусов равна 2а. Для любой другой точки эллипса сумма расстояний r1+r2 от нее до фокусов тоже равна 2а (рис. 6). Обычно эллипс так и определяют – как геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная(она равна 2а и она больше расстояния между фокусами, равного 2с). Каноническое уравнение эллипса можно вывести и из соотношения MF1+MF2=r1+r2=2a, используя, что F1F2=2c. Надо переписать его в координатной форме и избавиться от корней — перенести один из корней в правую часть уравнения, возвести обе части в квадрат, и еще раз избавиться от корня с помощью возведения в квадрат. Если исходить из этого определения, то то, что эллипс – сжатая окружность, выводится из его уравнения, как свойство.
Нормаль и касательная к эллипсу являются биссектрисами соответственно внутреннего и внешнего углов между радиусами-векторами, проведенными из точки касания в фокусы (рис 7). На чертеже видно, что луч, выходящий из F1, отразившись от касательный по формуле "угол падения равен углу отражения", попадает в фокус F2.
Если а>b, то эллипс вытянут вдоль оси X, и число а называют большой полуосью. И фокусы расположены на оси X. Если же b>а, то эллипс вытянут вдоль оси Y. И фокусы расположены на оси Y. Для него все рассуждения сохраняются, но с заменой в них x на y и а на b, соответственно. Очевидно, что если а=b, то фокусное расстояние обращается в ноль, фокусы совпадают и эллипс превращается в окружность с радиусом а и с центром в начале координат. Так что окружность – это частный случай эллипса (рис. 8).
 |
Уравнение 
— уравнение эллипса с центром в точке C(d,e).
Примеры
1.Составьте уравнение линии, полученной сжатием окружности х 2 +у 2 =25 по оси Y к оси Х с коэффициентом сжатия k, если k=35.
Решение. Заданная окружность вписывается в квадрат со стороной 5. Следовательно, большая полуось эллипса а=5. По условию задачи 
, отсюда b=3 и уравнение эллипса: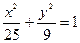 
2.При проектировании окружности на какую-нибудь плоскость Р диаметр АА1, параллельный этой плоскости, проектируется в натуральную величину. А все хорды, перпендикулярные к этому диаметру, сокращаются в отношении, равном cosj, где j — угол между плоскостью окружности Р1 и плоскостью Р. Поэтому проекция окружности есть эллипс с большой осью 2а=АА1 и коэффициентом сжатия k=cosj (малая полуось равна acosj) (рис. 9).
3. Эллипс используется в черчении для изображения окружности, расположенной не в плоскости чертежа, и в живописи при изображении окружности, не находящейся в плоскости, параллельной плоскости изображения (рис.10а). Шар изображают окружностью. Для того чтобы показать его объемность, в нем изображается "экватор" в виде эллипса и полюс Р (рис. 10б). Изображение полюсов получается параллельным переносом изображений полюсов на виде шара слева. Можно этот дополнительный чертеж не строить, а достаточно заметить, что из равенства: DО2СО=DР2РО=DР1РО=DQ1QО следует равенство: OC=OD=PP1=QQ1 и точки Р и Q выбираются так, чтобы выполнялись эти равенства.
Последнее изменение этой страницы: 2016-04-21; Нарушение авторского права страницы
Не могу найти формулы, как найти ширину и высоту вписанного в эллипс прямоугольника, зная вертикальный и горизонтальный радиусы эллипса и соотношения сторон прямоугольника.
Пример:
горизонтальный радиус = 10
вертикальный радиус = 5
ширина = 2 высоты
нужно найти значения высоты и ширины, если прямоугольника вписан в эллипс
Если есть готовая npm-библиотека с этими формулами или пример на JS, прошу подсказать.
Математиков прошу подсказать сами формулы, гугление предлагает мне только окружности с одним радиусом.
Всем спасибо!
Загрузка...
