Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что: а) одна из них обработана на 3-м станке;
б) обе обработаны на одном станке?
а) Обозначим события: Ai – деталь обработана на i-м станке (i = 1, 2, 3);
В – одна из двух взятых деталей обработана на 3-м станке.
Очевидно, что B=
A1
A3+
A2
A3+
A3
A1+
A3
A2 (при этом надо учесть, что либо первая деталь обработана на 3-м станке, либо вторая). По теоремам сложения и умножения (для независимых событий)
б) Пусть событие С – обе отобранные детали обработаны на одном станке. Тогда
C=
A1
A1+
A2
A2+
A3
A3 и P(C) = 0,1*0,1 + 0,3*0,3 + 0,6*0,6 = 0,46.
(при использовании теоремы умножения учли независимость событий A1 , A2 и А3 ).
Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что: а) одна из них обработана на 3-м станке;
б) обе обработаны на одном станке?
а) Обозначим события: Ai – деталь обработана на i -м станке (i = 1, 2, 3);
В – одна из двух взятых деталей обработана на 3-м станке.
По условию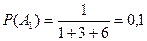 
, 
, 
.
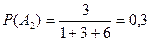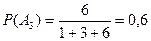Очевидно, что B= A1 A3 + A2 A3 + A3 A1 + A3 A2 (при этом надо учесть, что либо первая деталь обработана на 3-м станке, либо вторая). По теоремам сложения и умножения (для независимых событий)
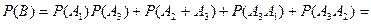
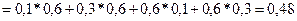
б) Пусть событие С – обе отобранные детали обработаны на одном станке. Тогда
Экзаменационный билет для письменного экзамена состоит из 10 вопросов – по 2 вопроса из 20 по каждой из пяти тем, представленных в билете. По каждой теме студент подготовил лишь половину всех вопросов. Какова вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на один вопрос по каждой из пяти тем в билете?
Обозначим события: А1 , А2 – студент подготовил 1-й, 2-й вопросы билета по каждой теме;
Bi – студент подготовил хотя бы один вопрос билета из двух по i -й теме (i = 1, 2, . 5);
С – студент сдал экзамен.
В силу условия С = В1 В2 В3 В4 B5 . Полагая ответы студента по разным темам независимыми, по теореме умножения вероятностей (1.24)
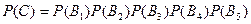
Так как вероятности Р(В i) (i =1,2. 5) равны, то P(C) = (Р(В i)) 5 . Вероятность Р(В i) можно найти по формуле (1.27) (или (1.25)):
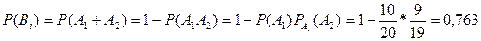
Теперь P(C) = 0,763 5 = 0,259
При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что:
а) двигатель начнет работать при третьем включении зажигания;
б) для запуска двигателя придется включать зажигание не более трех раз.
а) Обозначим события: А – двигатель начнет работать при каждом включении зажигания;
В – то же при третьем включении зажигания.
Очевидно, что В=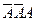 
и Р(В) = 
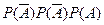= 0,4*0,4*0,6 = 0,096.
б) Пусть событие С – для запуска двигателя придется включать зажигание не более трех раз. Очевидно, событие С наступит, если двигатель начнет работать при 1-м включении, или при 2-м, или при 3-м включении, т.е. С = А + АА + А АА. Следовательно,
О Пример 1.26. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй — 0,9; третий — 0,8. Найти вероятность того, что студентом будут сданы: а) только 2-й экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
Решение, а) Обозначим события: Л, — студент сдаст г-й экзамен (г = 1, 2,3); В — студент сдаст только 2-й экзамен из трех. Очевидно, что 
т.е.
совместное осуществление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й экзамены. Учитывая, что события Ах, Л2, Л3 независимы, получим
б) Пусть событие С — студент сдаст один экзамен из трех. Очевидно, событие С произойдет, если студент сдаст только 1-й экзамен из трех, или только 2-й, или только 3-й, т.е.
в) Пусть событие О — студент сдаст все три экзамена, т.е. О = А1А2А3. Тогда 
г) Пусть событие Е — студент сдаст по крайней мере два экзамена (иначе: «хотя бы два» экзамена или «не менее двух» экзаменов). Очевидно, что событие Е означает сдачу любых двух экзаменов из трех либо всех трех экзаменов, т.е.
д) Пусть событие Т — студент сдаст хотя бы один экзамен (иначе:
«не менее одного» экзамена). Очевидно, событие Б представляет сумму событий С (включающего три варианта) и Е (четыре варианта), т.е. Е=АХ + + Л2 + Л3 = С + Е (семь вариантов). Однако проще найти вероятность события У 7 , если перейти к противоположному событию, включающему всего один вариант — 
, т.е. применить формулу (1.27).
т.е. сдача студентом хотя бы одного экзамена из трех является событием практически достоверным. ?
[> Пример 1.27. Причиной разрыва электрической цепи служит выход из строя элемента Кх или одновременный выход из строя двух элементов — К2 и /С3. Элементы могут выйти из строя независимо друг от друга с вероятностями, равными соответственно 0,1; 0,2; 0,3. Какова вероятность разрыва электрической цепи?Решение. Обозначим события:
Л, — выход из строя элемента К< (г = 1, 2, 3);
В — разрыв электрической цепи.
Очевидно, по условию событие В произойдет, если произойдет либо событие Аи либо Л^, т.е. В = А] + А^А3. Теперь, по формуле (1.25)
(при использовании теоремы умножения учли независимость событий Ах,
[> Пример 1.28. Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что:а) одна из них обработана на 3-м станке; б) обе обработаны на одном станке?
Решение, а) Обозначим события:
Л, — деталь обработана на ?-м станке (г = 1, 2, 3);
В — одна из двух взятых деталей обработана на 3-м станке.
Очевидно, что В =АХА3 + Л2Л3 + Л3Л х + Л3Л2 (при этом надо учесть, что либо первая деталь обработана на 3-м станке, либо вторая). По теоремам сложения и умножения (для независимых событий)
б) Пусть событие С — обе отобранные детали обработаны на одном станке. Тогда 
и
О Пример 1.29. Экзаменационный билет для письменного экзамена состоит из 10 вопросов — но 2 вопроса из 20 по каждой из пяти тем, представленных в билете. По каждой теме студент подготовил лишь половину всех вопросов. Какова вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на один вопрос по каждой из пяти тем в билете?
Решение. Обозначим события:
А<,А2 — студент подготовил 1-й, 2-й вопросы билета по каждой теме;
5, — студент подготовил хотя бы один вопрос билета из двух но ?-й теме 0 = 1,2. 5);
С — студент сдал экзамен.
В силу условия 
Полагая ответы студента по разным
темам независимыми, по теореме умножения вероятностей (1.24)
Так как вероятности Р(В,) (г = 1,2. 5) равны, то 
Вероятность Р(В) можно найти по формуле (1.27) (или (1.25)):
Теперь ? 
1> Пример 1.30. При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что: а) двигатель начнет работать при третьем включении зажигания; б) для запуска двигателя придется включать зажигание не более трех раз.
Решение. а) Обозначим события:
А — двигатель начнет работать при каждом включении зажигания;
В — то же при третьем включении зажигания.
Очевидно, что 
б) Пусть событие С — для запуска двигателя придется включать зажигание не более трех раз. Очевидно, событие С наступит, если двигатель начнет работать при 1-м включении, или при 2-м, или при 3-м включении, т.е.
Следовательно,
> Пример 1.31. Среди билетов денежно-вещевой лотереи половина выигрышных. Сколько лотерейных билетов нужно купить, чтобы с вероятностью, не меньшей 0,999, быть уверенным в выигрыше хотя бы по одному билету?
Решение. Пусть вероятность события — выигрыша по /-му билету равна Ру т.е. Р(А,) -р. Тогда вероятность выигрыша хотя бы по одному из п приобретенных билетов, т.е. вероятность суммы независимых событий Л2. А,,
. Ап определится по формуле (1.29):
По условию 
откуда
Логарифмируя обе части неравенства, имеем
Учитывая, что ^ (1 — р) — величина 
отрицательная, получим
По условию р = 0,5, = 0,999. По формуле (1.30) 
т.е.
п > 10 и необходимо купить не менее 10 лотерейных билетов.
(Задачу можно решить, не прибегая к логарифмированию, путем подбора целого числа я, при котором выполняется неравенство 
т.е. в данном случае 
; так, еще при 
а уже при 
т.е. п > 10). ?
О Пример 1.31а. Среди клиентов банка 80% являются физическими лицами и 20% — юридическими. Из практики известно, что 40% всех операций приходится на долгосрочные расчеты, в то же время из общего числа операций, связанных с физическими лицами, 30% приходится на долгосрочные расчеты. Какова вероятность того, что наудачу выбранный клиент является юридическим лицом и осуществляет долгосрочный расчет?
Решение. Обозначим события:
А — клиент является физическим лицом;
В — клиент осуществляет долгосрочный расчет.
По условию Р(А) = 0,8; Р(Л) = 0,2; Р(В) = 0,4; РА(В) = 0,3. Требуется найти вероятность совместного осуществления событий А и Б, т.е. Р<АВ).
Так как В = АВ + АВ, то
О Пример 1.32. Два игрока поочередно бросают игральную кость. Выигрывает тот, у которого первым выпадет «6 очков». Какова вероятность выигрыша для игрока, бросающего игральную кость первым? Вторым?
Решение. Обозначим события:
Л; — выпадение 6 очков при г’-м бросании игральной кости (г = 1, 2. );
В — вышрыш игры игроком, бросающим игральную кость первым.
Имеем Р <А,) —1/6, Р(Л,) = 5/б при любом I
Событие В можно представить в виде суммы вариантов:
Поэтому
По формуле суммы геометрического ряда с первым членом а = 1/6 и знаменателем г/ = (5/6) 2 Пример 1.33а. Вероятность того, что студент сдаст экзамен по дисциплине Л, равна 0,8. Условная вероятность того, что студент сдаст экзамен по дисциплине В, равна: 0,5 при условии, что он экзамен по дисциплине А сдаст; 0,6 при условии — что не сдаст.
- 1) Найти вероятность того, что экзамен хотя бы по одной из двух дисциплин студент: а) сдаст; б) не сдаст.
- 2) Являются ли события — сдача экзамена по дисциплинам А и В независимыми?
Решение. 1) Пусть события А и В означают, что студент сдаст экзамены по дисциплинам А и В. По условию требуется найти Р(А + В) и 
I,
если известно, что 
где 
Теперь по формуле (1.25)
Согласно закону де Моргана 
, поэтому 
то по любому из этих оснований события А и В зависимы. ?
[> Пример 1.34. На рис. 1.7 представлены приборы, состоящие из четырех блоков, каждый из которых имеет надежность (вероятность безотказной работы в течение некоторого периода времени) р = 0,9. Блоки выходят из строя независимо друг от друга. Найти надежность каждого прибора. 
Решение, а) При последовательном соединении блоков (рис. 1.7, а) прибор будет безотказно работать в случае безотказной работы всех четырех блоков, поэтому надежность прибора определяется по теореме умножения вероятностей (1.24) для независимых событий:
б) При параллельном соединении блоков (рис. 1.7, в) прибор будет безотказно работать в случае безотказной работы хотя бы одного из четырех блоков, поэтому надежность прибора определяется по формуле вероятности суммы совместных независимых событий (1.29):
в) При «смешанном» соединении блоков (рис. 1.7, в) надежность прибора, очевидно, равна:
Как видим, наибольшую надежность имеет параллельное соединение блоков. ?
Загрузка...
