Проверка графа на ацикличность

Пусть дан ориентированный или неориентированный граф без петель и кратных рёбер. Требуется проверить, является ли он ациклическим, а если не является, то найти любой цикл.

Решим эту задачу с помощью поиска в глубину за O (M).

Алгоритм

Произведём серию поисков в глубину в графе. Т.е. из каждой вершины, в которую мы ещё ни разу не приходили, запустим поиск в глубину, который при входе в вершину будет красить её в серый цвет, а при выходе — в чёрный. И если поиск в глубину пытается пойти в серую вершину, то это означает, что мы нашли цикл (если граф неориентированный, то случаи, когда поиск в глубину из какой-то вершины пытается пойти в предка, не считаются).

Сам цикл можно восстановить проходом по массиву предков.

Реализация

Здесь приведена реализация для случая ориентированного графа.

Итак, я сделал следующий код для DFS:

Теперь я прочитал, что в неориентированном графе, если во время DFS он снова возвращается в ту же самую вершину, возникает цикл. Поэтому я сделал это,

Но моя функция checkcycle возвращает true, даже если их нет. Это почему? Что-то не так с моей функцией? Нет проблем с выполнением, иначе я бы отладил, но, похоже, что-то не так в моей логике.

Решение

Обратите внимание, что ваша функция не совсем делает то, что вы думаете. Позвольте мне попытаться пройти через то, что здесь происходит. Предположим следующие соотношения: (1,2), (1,3), (2,3). Я не предполагаю возвратности (то есть (1,2) не подразумевает (2,1)). Отношения направлены.

1. Начните с узла 1. Отметьте его как посещенный
2. Итерируйте своих детей (2 и 3)
3. Когда в узле 2, рекурсивный вызов check cycle , В этот момент 2 также помечается как посещенный.
4. Теперь рекурсивный вызов посещает 3 (поиск DEPTH). 3 также помечен как посещенный
5. Призыв к шагу 4 умирает, возвращаясь false
6. Призыв к шагу 3 умирает, возвращаясь false
7. Мы вернулись к шагу 2. Теперь мы будем повторять узел 3, который уже был помечен на шаге 4. Он просто возвращает true ,

Вам нужен стек посещенных узлов, или вы ТОЛЬКО ищете исходный узел. Стек также обнаруживает подциклы (циклы, которые не включают в себя исходный узел), но он также занимает больше памяти.

Изменить: стек узлов не просто куча true / false значения, но вместо этого стека номеров узлов. Узел был посещен в текущей трассировке стека, если он присутствует в стеке.

Однако есть более дружественный способ памяти: set arr[foo] = false; как звонки умирают. Что-то вроде этого:

Я думаю, этого должно быть достаточно.

Редактировать: теперь должен поддерживать неориентированные графы.
Узел: этот код не проверен

Изменить: для более сложных решений см. Сильно связанные компоненты

Изменить: этот ответ является рыночным, как принято, хотя конкретное решение было дано в комментариях. Прочитайте комментарии для деталей.

Другие решения

все ли значения bool в arr [] установлены в false перед началом проверки?

Вы уверены, что ваш итератор для узлов не дублирует ребра, которые он уже прошел (и, таким образом, видит начальный узел несколько раз независимо от циклов)?

Содержание

Алгоритм [ править ]

Будем решать задачу с помощью поиска в глубину.

В случае ориентированного графа произведём серию обходов. То есть из каждой вершины, в которую мы ещё ни разу не приходили, запустим поиск в глубину, который при входе в вершину будет красить её в серый цвет, а при выходе из нее — в чёрный. И, если алгоритм пытается пойти в серую вершину, то это означает, что цикл найден.

В случае неориентированного графа, одно ребро не должно встречаться в цикле дважды по определению. Поэтому необходимо дополнительно проверять, что текущее рассматриваемое из вершины ребро не являетя тем ребром, по которому мы пришли в эту вершину.

Заметим, что, если в графе есть вершины с петлями, то алгоритм будет работать корректно, так как при запуске поиска в глубину из такой вершины, найдется ребро, ведущее в нее же, а значит эта петля и будет являться циклом.

Для восстановления самого цикла достаточно при запуске поиска в глубину из очередной вершины добавлять эту вершину в стек. Когда поиск в глубину нашел вершину, которая лежит на цикле, будем последовательно вынимать вершины из стека, пока не встретим найденную еще раз. Все вынутые вершины будут лежать на искомом цикле.

Асимптотика поиска цикла совпадает с асимптотикой поиска в глубину — [math]O(|V| + |E|)[/math] .

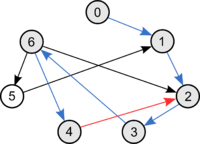
Доказательство [ править ]

Пусть дан граф [math]G[/math] . Запустим [math]mathrm(G)[/math] . Рассмотрим выполнение процедуры поиска в глубину от некоторой вершины [math] v [/math] . Так как все серые вершины лежат в стеке рекурсии, то для них вершина [math] v [/math] достижима, так как между соседними вершинами в стеке есть ребро. Тогда, если из рассматриваемой вершины [math] v [/math] существует ребро в серую вершину [math] u [/math] , то это значит, что из вершины [math] u [/math] существует путь в [math] v [/math] и из вершины [math] v [/math] существует путь в [math] u [/math] состоящий из одного ребра. И так как оба эти пути не пересекаются, то цикл существует.

Докажем, что если в графе [math]G[/math] существует цикл, то [math]mathrm(G)[/math] его всегда найдет. Пусть [math] v [/math] — первая вершина принадлежащая циклу, рассмотренная поиском в глубину. Тогда существует вершина [math] u [/math] , принадлежащая циклу и имеющая ребро в вершину [math] v [/math] . Так как из вершины [math] v [/math] в вершину [math] u [/math] существует белый путь (они лежат на одном цикле), то по лемме о белых путях во время выполнения процедуры поиска в глубину от вершины [math] u [/math] , вершина [math] v [/math] будет серой. Так как из [math] u [/math] есть ребро в [math] v [/math] , то это ребро в серую вершину. Следовательно [math]mathrm(G)[/math] нашел цикл.