Проверка на выпуклость многоугольника по координатам

Всем доброго дня, есть задача определить выпуклость многоугольника. Пробовал через площади прямоугольников, достроенных от точек. Код выглядит приблизительно так.

Разумеется не сработало, многоугольник задаю таким образом:

Смотрел реализации других людей, данной проверки(на выпуклость), но выходило, либо слишком громоздко, либо не мог адаптировать под свои структуры. Жду конструктивной критики и попыток помочь.

2 ответа 2

Многоугольник будет выпуклым если при его обходе в каждой тройке последовательных вершин происходит поворот всегда в одну и ту же сторону. При обходе многоугольника против часовой стрелке поворот будет всегда налево, а при обходе по часовой — направо.

Если одно ребро многоугольника соответствует вектору AB , а следующее за ним ребро соответствует вектору BC , то направление поворота в этой паре последовательных ребер будет задаваться знаком выражения

Для поворота налево это значение будет положительным, а для поворота направо — отрицательным (я предполагаю, что ось Y направлена вверх). Нулевое значение означает, что ребра коллинеарны.

Это дает нам алгоритм определения выпуклости. Для каждой вершины i нам надо вычислить

(Разумеется, надо быть аккуратным при вычислении индексов соседних точек i — 1 и i + 1 на краях массива)

По поведению знака величины product на всех вершинах многоугольника мы и получим ответ на наш вопрос о выпуклости.

Опять же, если заранее известно, что многоугольник обходится против часовой стрелки, то встретив первое отрицательное product , вы можете сразу говорить, что многоугольник невыпукл.

Если направление обхода заранее неизвестно, то придется проверить все вершины и убедиться, что знаки величины product везде одинаковы (и не забыть аккуратно обработать нулевое значение).

Определение выпуклости многоугольника.

Алгоритм Кируса–Бэка предполагает наличие выпуклого многоугольника, используемого в качестве окна.

Однако на практике весьма часто возникает задача отсечения многоугольником, а информация о том, является он выпуклым или нет изначально не задается. В таком случае, прежде чем начать процедуру отсечения необходимо определить какой задан многоугольник – выпуклый или нет.

Дадим некотрые определения выпуклости многоугольника

Выпуклым считается многоугольник, для которого выполняется одно из ниже перечисленных условий:

1) в выпуклом многоугольнике все вершины располагаются по одну сторону от линии, несущей любое ребро (по внутреннюю сторону относительно данного ребра);

2) все внутренние углы многоугольника меньше 180 о ;

3) все диагонали, связывающие вершины многоугольника, лежат внутри этого многоугольника;

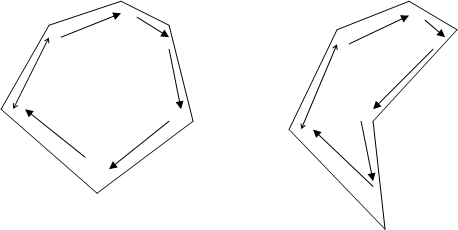
4) все углы многоугольника обходятся в одном направлении (Рис. 3.3‑1).

Для выработки аналитического представление последнего критерия выпуклости, используем векторное произведение.

Векторное произведение W двух векторов a и b (Рис. 3.3‑2 а) определяется как:

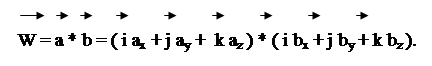— a_x , a_y , a_z и b_x , b_y , b_z являются проекциями на оси координат X , Y , Z , соответственно, векторов – сомножителей a и b ,

— i , j , k – единичные векторы по координатным осям X , Y , Z .

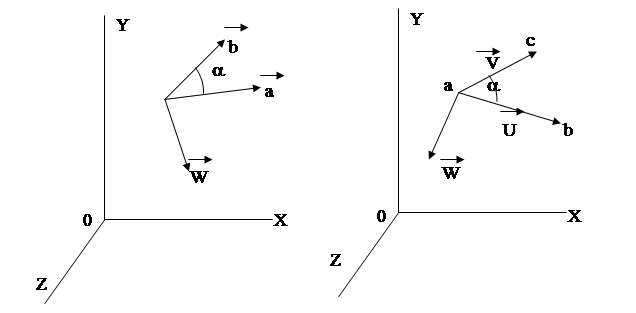
Если рассматривать двумерное представление многоугольника как представление его в координатной плоскости XY трехмерной системе координат X , Y , Z (Рис. 3.3‑2 b ), то выражение для формирования векторного произведения векторов U и V , где векторы U и V являются соседними ребрами, образующими угол многоугольника, можно записать в виде определитель:

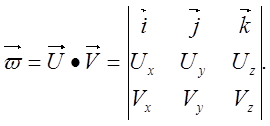
Вектор векторного произведения перпендикулярен плоскости, в которой находятся вектора-сомножители. Направление вектора произведения определяется по правилу буравчика или по правилу винта с правой нарезкой.

Для случая, представленного на Рис. 3.3‑2 b ), вектор W , соответствующий векторному произведению векторов V , U , будет иметь ту же направленность, что и направленность координатной оси Z .

Учитывая то, что проекции на ось Z векторов –сомножителей в этом случае равны нулю, векторное произведение можно представить в виде:

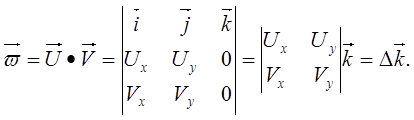(3.3-1)

Единичный вектор k всегда положительный, следовательно, знак вектора w векторного произведения будет определяться только знаком определителя D в выше приведенном выражении. Отметим, что на основании свойства векторного произведения, при перестановке местами векторов-сомножителей U и V знак вектора w будет меняться на противоположный.

Отсюда следует, что, если в качестве векторов V и U рассматривать два соседних ребра многоугольника, то порядок перечисления векторов в векторном произведении можно поставить в соответствие c обходом рассматриваемого угла многоугольника или ребер, образующих этот угол. Это позволяет использовать в качестве критерия определения выпуклости многоугольника правило:

если для всех пар ребер многоугольника выполняется условие:

Если знаки векторных произведений для отдельных углов не совпадают, то многоугольник не выпуклый.

Так как ребра многоугольник задаются в виде координат их концевых точек, то для определения знака векторного произведения удобнее использовать определитель:

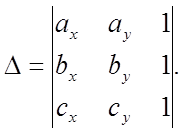
Легко показать, что этот определитель эквивалентен определителю в выражении (3.3-1).

Рассмотрим простую задачу расчета площади треугольника по его координатам через матрицу.

В принципе, мы это обсуждали в статье, но хотелось обратить Ваше внимание на одно замечательное свойство, которое нам пригодится в строительстве дальнейших калькуляторов.

Напомним, что площадь треугольника через координаты вершин вычисляется

Вспомнив, а кто не знает может ознакомится с свойствами определителя, заметим, что смена строк ( например вторую на первую) меняет знак определителя на противоположный. И хотя площадь треугольника не может быть отрицательным числом( поэтому он отбрасывается при вычислении площади), отсюда следует важное свойство!

Геометрически,смена знака означает, что мы меняем "путь обхода" вершин треугольника. То есть при обходе вершин треугольника по часовой стрелке, получается один знак (отрицательный), при обходе вершин треугольника против часовой стрелки, знак определителя будет противоположный (положительный).

Где же это можно применить?

Нам это свойство пригодится для расчетов многоугольников, определить какие части его выпуклые, а какие впалые ("впуклые" 🙂 ). Для разбиения многоугольника на треугольники, это незаменимая задача.

Например при правильном многоугольника ( а это фигура выпуклая) все знаки будут одинаковы.

При вычислении трапеции, тоже все знаки будут одинаковы.

А вот при вычислении фигуры в виде звезды, знаки будут менятся с плюса на минус и так далее, в зависимости от количества лучей в звезде.

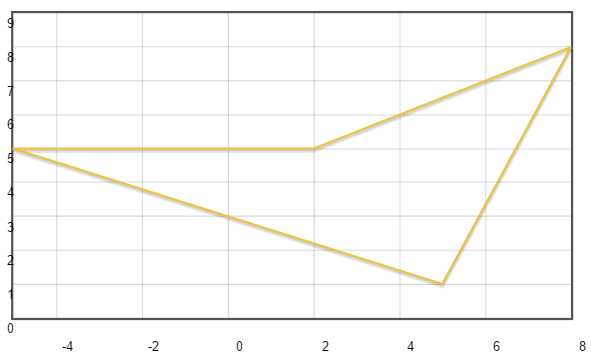
Рассмотрим многоугольник с координатами 5:1 8:8 2:5 -5:5

Читайте также Рамка для текста деньги