
2.81. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули m, = 5 г, масса шара m2 = 0.5 кг. Скорость пули V, = 500-м/с. При каком предельном расстоянии / от центра шара до точки подвеса стержня шар от удара пули поднимется до верхней точки окружности?

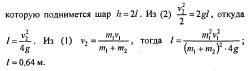
2.82. Деревянным молотком, масса которого m, = 0,5 кг, ударяют о неподвижную стенку. Скорость молотка в момент удара v, = 1 м/с. Считая коэффициент восстановления при ударе молотка о стенку к — 0,5, найти количество теплоты Q, выделившееся при ударе. (Коэффициентом восстановления материала тела называют отношение скорости после удара к его скорости до удара.)

2.83. В условиях предыдущей задачи найти импульс силы Fdt, полученный стенкой за время удара.

2.84. Деревянный шарик массой m = 0,1 кг падает с высоты h1 = 2 м. Коэффициент восстановления при ударе шарика о пол к = 0,5. Найти высоту h,, на которую поднимется шарик после удара о пол, и количество теплоты Q, выделившееся при ударе.
Пуля, летящая горизонтально, попадает в шар, подвешенный на лёгком жёстком стержне, и застревает в нём. Масса пули в 1000 раз меньше массы шара. Расстояние от точки подвеса стержня до центра шара равно 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара на угол 10о.
Если пуля застревает в шаре, то удар
абсолютно неупругий, и выполняется только закон сохранения импульса. До удара пуля имела импульс mυ, шар импульса не имел. Непосредственно после удара пуля с шаром имеют общую скорость υ1, их импульс (M + m) υ1.
Закон сохранения импульса:
Шар вместе с пулей в момент удара приобрёл кинетическую энергию:
За счёт этой энергии шар поднялся на высоту h, при этом его кинетическая энергия переходит в потенциальную:
Ek = Eп Þ = (M + m) gh. (9)
Высоту h можно выразить через расстояние от точки подвеса до центра шара и угол отклонения от вертикали
h = L – L cos a = L(1 – cos a ).
Подставив последнее выражение в соотношение (9), получим:
a L = gL(1 – cos a ),
h и определим скорость пули:
Подставив числовые значения, получим:
υ = 1001 » 543 м/с.
Камень, привязанный к верёвке, равномерно вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжениями верёвки равны 9,8 Н.
В верхней точке траектории и сила тяжести, и сила натяжения верёвки направлены вниз.
L Уравнение движения в верхней точке имеет вид:
L man = m = mg + T1.
В нижней точке траектории сила тяжести направлена вниз, а сила натяжения верёвки и нормальное ускорение вверх. Уравнение движения в нижней точке:
По условию камень вращается с постоянной скоростью, поэтому левые части обоих уравнений одинаковы. Значит, можно приравнять правые части:
отсюда T2 – T1 = 2mg,
Подставляем числа: m = = 0,5 кг.
Шоссе имеет вираж с уклоном в 10° при радиусе закругления дороги в 100 м. На какую скорость рассчитан вираж?
Сила, действующая на автомобиль, складывается
из силы тяжести и силы нормального давления . Сумма этих сил обусловливает нормальное ускорение автомобиля при повороте.
Шар массой кг подвешен на невесомом жестком стержне длиной м, шарнирно закрепленном за верхний конец. В шар попадает пуля массой г, летящая со скоростью м/с под углом к горизонту, и застревает в нем. Определить максимальный угол отклонения стержня от вертикали. Ускорение свободного падения м/c .
Пусть модуль скорости шара с застрявшей в нем пулей непосредственно после соударения. По закону сохранения импульса в проекции на горизонтальное направление имеем:
При движении шара с пулей после соударения сохраняется механическая энергия, откуда следует, что высота подъема шара над нижней точкой


