Радиус вписанной сферы в правильную треугольную пирамиду

Биссекторная плоскость. Основное свойство биссекторной плоскости

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Радиус сферы, вписанной в правильную n — угольную пирамиду

Сфера, вписанная в треугольную пирамиду. Формула для радиуса вписанной сферы

Биссекторная плоскость. Основное свойство биссекторной плоскости

Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).

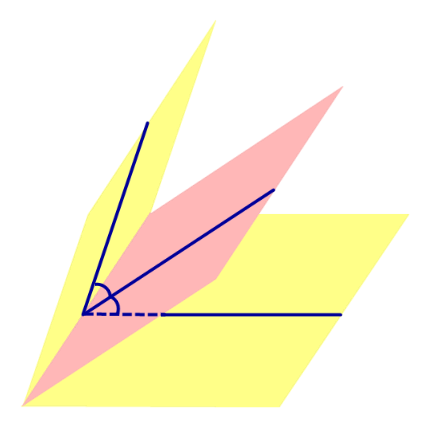
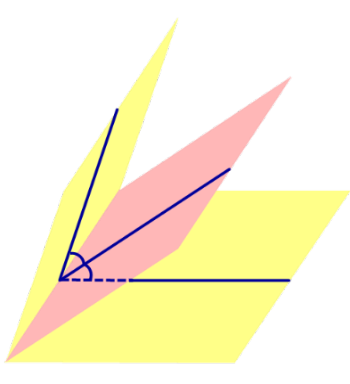
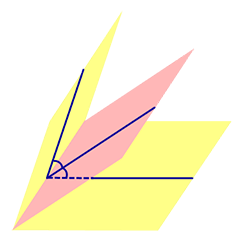
Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.

Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ , перпендикулярную к ребру AB двугранного угла (рис. 2).

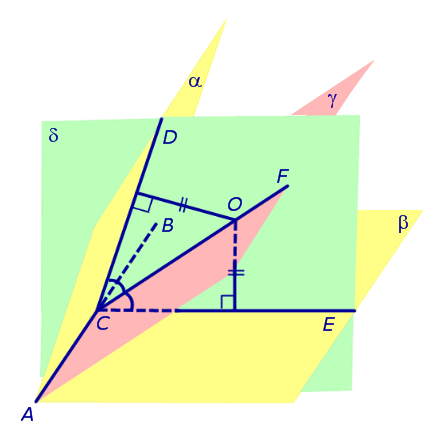
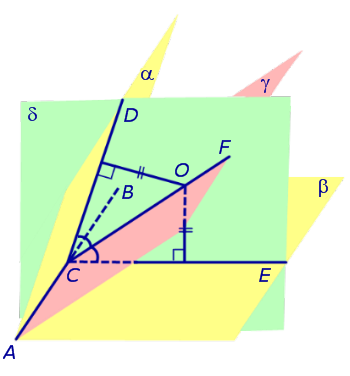
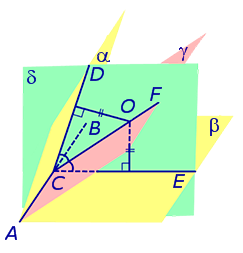
Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .

Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.

Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

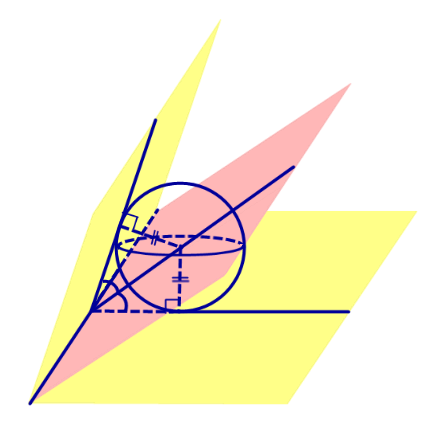
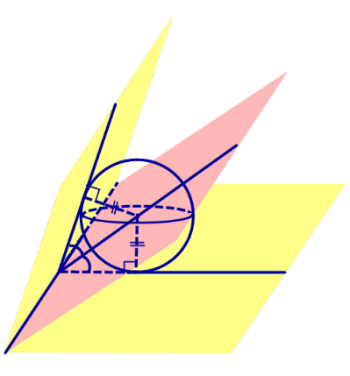
Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

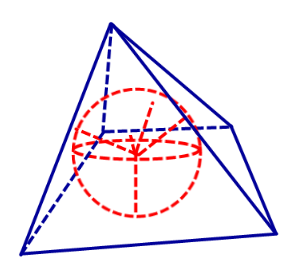
Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

Утверждение 2. Если у пирамиды SA₁A₂ . A_n основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A₁A₂ . A_n , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.

Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA₁A₂ и проведем в ней высоту SB (рис. 5).

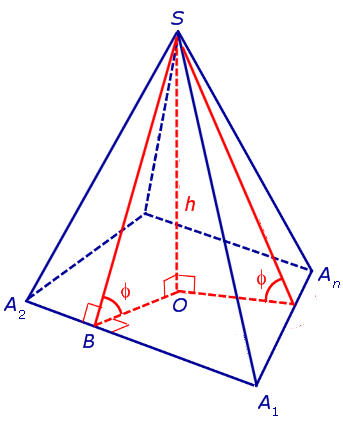
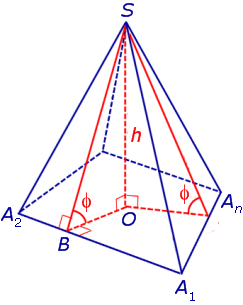
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A₁A₂ . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA₁A₂ и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).

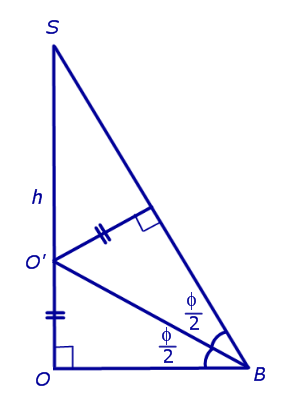
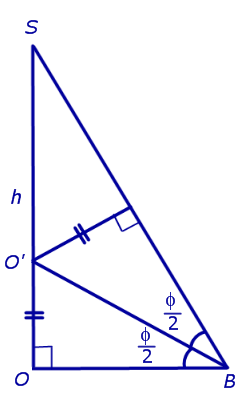
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле

Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле

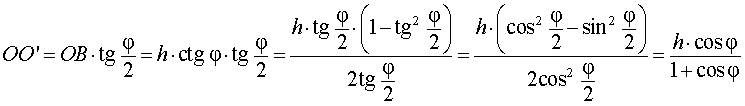
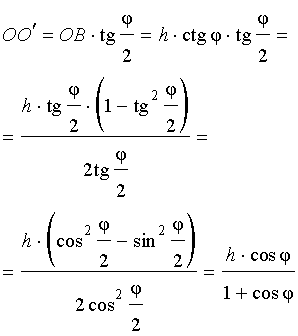
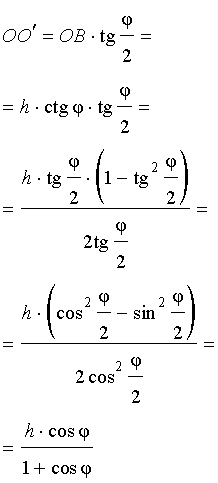
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.

Доказательство утверждения 2 завершено.

Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле

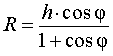(1)

Радиус сферы, вписанной в правильную n — угольную пирамиду

Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).

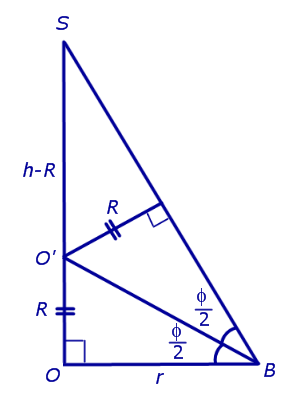
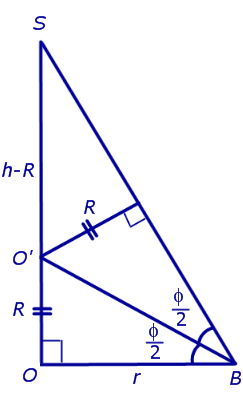
Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем

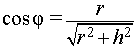(2)

В силу следствия 2 из формул (1) и (2) получаем

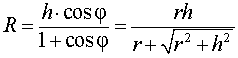
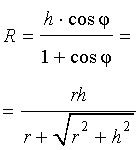
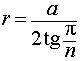
из формулы (3) получаем соотношение

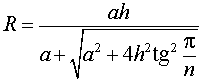
Ответ.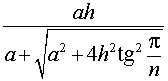

Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен

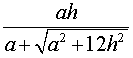
Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен

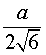
Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен

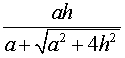
Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен

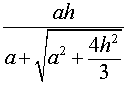
Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы

Утверждение 3. В любую треугольную пирамиду можно вписать сферу.

Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.

Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).

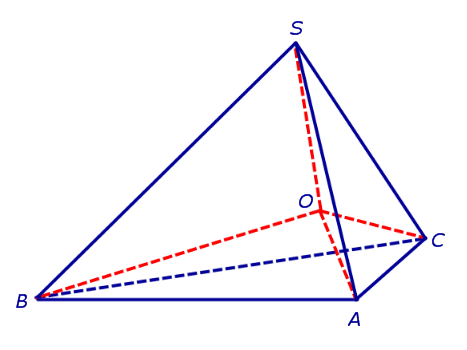
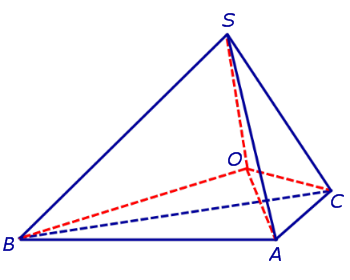
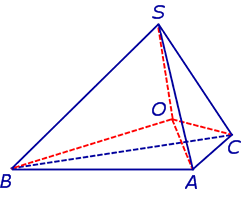
Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами

а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами

то справедливы следующие равенства:

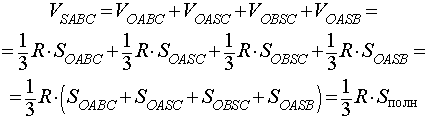
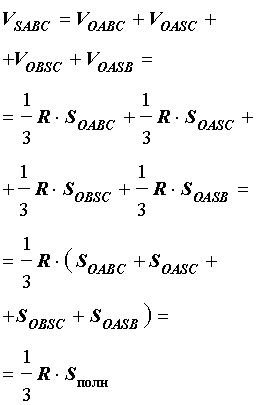
где символом S_полн обозначена площадь полной поверхности пирамиды SABC.

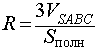
Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы

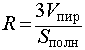
где символами V_пир и S_полн обозначены объем и площадь полной поверхности пирамиды соответственно.

Знание — сила. Познавательная информация

Шар, вписанный в пирамиду

Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.

Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).

Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.

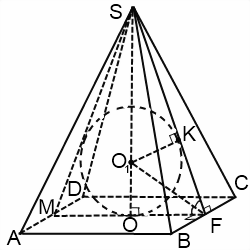
Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.

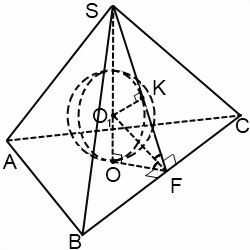
Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.

В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.

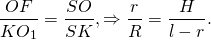
В треугольнике SOF применим свойство биссектрисы треугольника:

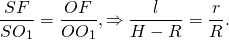
Из прямоугольного треугольника OO1F

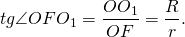
При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.

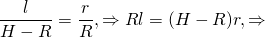
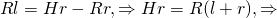
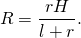
Теперь найдем отношение объема пирамиды к площади ее поверхности:

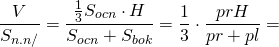
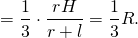
Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:

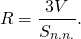
Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны ).

уЖЕТБ ЧРЙУБОБ Ч РТБЧЙМШОХА ФТЕХЗПМШОХА РЙТБНЙДХ SABC ( S – ЧЕТЫЙОБ), Б ФБЛЦЕ ЧРЙУБОБ Ч РТСНХА ФТЕХЗПМШОХА РТЙЪНХ KLMK 1L 1M 1 , Х ЛПФПТПК KL=KM= , Б ВПЛПЧПЕ ТЕВТП KK 1 МЕЦЙФ ОБ РТСНПК AB . оБКДЙФЕ ТБДЙХУ УЖЕТЩ, ЕУМЙ ЙЪЧЕУФОП, ЮФП РТСНБС SC РБТБММЕМШОБ РМПУЛПУФЙ LL 1M 1M .
фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

тЕЫЕОЙЕ

юЕТЕЪ РТСНХА, ОЕ ЙНЕАЭХА УП УЖЕТПК ПВЭЙИ ФПЮЕЛ, НПЦОП РТПЧЕУФЙ ТПЧОП ДЧЕ РМПУЛПУФЙ, ЛБУБАЭЙЕУС УЖЕТЩ, РПЬФПНХ РМПУЛПУФЙ ЗТБОЕК ABC Й KMM 1K 1 УПЧРБДБАФ, Б ФБЛЦЕ УПЧРБДБАФ РМПУЛПУФЙ ЗТБОЕК ASB Й KLL 1K 1 . гЕОФТ O УЖЕТЩ, ЧРЙУБООПК Ч РТБЧЙМШОХА РЙТБНЙДХ МЕЦЙФ ОБ ЕЈ ЧЩУПФЕ (ТЙУ.1). тБУУНПФТЙН УЕЮЕОЙЕ РЙТБНЙДЩ Й РТЙЪНЩ РМПУЛПУФША, РТПИПДСЭЕК ЮЕТЕЪ ЧЩУПФХ SH РЙТБНЙДЩ Й ЕЈ ВПЛПЧПЕ ТЕВТП SC . ч ЬФПК РМПУЛПУФЙ МЕЦЙФ ГЕОФТ O УЖЕТЩ Й УЕТЕДЙОБ K 2 ТЕВТБ AB . рМПУЛПУФШ УЕЮЕОЙС РТПЧЕДЕОБ ЮЕТЕЪ РТСНХА SC , РБТБММЕМШОХА РМПУЛПУФЙ LL 1M 1M , ЪОБЮЙФ, УЕЛХЭБС РМПУЛПУФШ РЕТЕУЕЛБЕФ РМПУЛПУФШ LL 1M 1M РП РТСНПК, РБТБММЕМШОПК SC . рПЬФПНХ, ЕУМЙ L 2 Й M 2 – ФПЮЛЙ, Ч ЛПФПТЩИ УЕЛХЭБС РМПУЛПУФШ РЕТЕУЕЛБЕФ ВПЛПЧЩЕ ТЈВТБ LL 1 Й MM 1 РТЙЪНЩ, ФП L 2M 2 || SC . рТЙ ЬФПН УЕЮЕОЙЕ УЖЕТЩ РТПЧЕДЈООПК РМПУЛПУФША – ПЛТХЦОПУФШ, ЧРЙУБООБС Ч ФТЕХЗПМШОЙЛ K 2L 2M 2 (ТЙУ.2), Ч ЛПФПТПН K 2L 2=K 2M 2= , Б Ф.Л. L 2M 2 || SC , ФП SK 2= CK 2 . чЩУПФБ SK 2 ТБЧОПВЕДТЕООПЗП ФТЕХЗПМШОЙЛБ ASB ТБЧОБ ЧЩУПФЕ CK 2 ТБЧОПУФПТПООЕЗП ФТЕХЗПМШОЙЛБ ABC , РПЬФПНХ ABS – ФБЛЦЕ ТБЧОПУФПТПООЙК ФТЕХЗПМШОЙЛ, Б РТБЧЙМШОБС РЙТБНЙДБ SABC – РТБЧЙМШОЩК ФЕФТБЬДТ. пВПЪОБЮЙН SK 2C = β , AB = SC = a . йЪ РТСНПХЗПМШОПЗП ФТЕХЗПМШОЙЛБ SHK 2 ОБИПДЙН, ЮФП
tg β = = = 2 .
фПЗДБ
cos β = = = , sin β = , sin = = = ,

L 2M 2 = 2K 2L 2 sin = 2 · =2 .
рХУФШ r – ТБДЙХУ УЖЕТЩ ЧРЙУБООПК Ч РТБЧЙМШОЩК ФЕФТБЬДТ SABC . фПЗДБ r – ТБДЙХУ ПЛТХЦОПУФЙ ЧРЙУБООПК Ч ФТЕХЗПМШОЙЛ K 2L 2M 2 . уМЕДПЧБФЕМШОП,
r = = =

фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

«>