Фиксируем переменную $ y $ и выполняем дифференцирование по $ x $:
$$ z’_x (y = const) = cos x cos y $$
Считаем постоянной $ x $ и находим производную по $ y $:
Частные производные  и
и 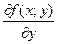 называют частными производными первого порядка. Их можно рассматривать как функции от
называют частными производными первого порядка. Их можно рассматривать как функции от  . Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
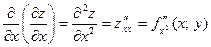 ;
;
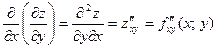 ;
;
 ;
;
 .
.
Аналогично определяются частные производные 3-го, 4-го и т.д. порядков
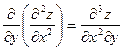 ,
, 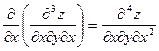 и т.д.
и т.д.
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной.
Теорема (Шварца). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой. В частности, для 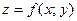 имеем:
имеем:  .
.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9621 —  | 7515 —
| 7515 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
2.7. Частные производные высших порядков
Пусть в некоторой области задана функция двух переменных z = f(x,y). Частные производные f ¢ x (x, y) и f ¢ y (x, y) в общем случае сами являются функциями переменных х и у, а потому допускают дифференцирование по каждой из переменных. В отличие от f ¢ x (x, y), f ¢ y (x, y) производные, полученные повторным дифференцированием функции z = f(x, y), принято называть производными высших порядков.
Частная производная (если она существует) от частной производной первого порядка функции z = f(x,y) называется частной производной второго порядка.
Дифференцируя f ¢ x (x, y) по х и по у, получим две частные производные второго порядка, которые обозначаются следующим образом:
 ,
,  .
.
 ,
,  .
.
Производные f ¢ ¢ xy и f ¢ ¢ yx называются смешанными производными, они отличаются тем, что первая получена дифференцированием функции z = f(x,y) сначала по х, а затем по у, вторая, наоборот, – сначала по у, затем по х.
Пример 8. Найти частные производные второго порядка функции z = sin(xy).
Решение. Находим сначала частные производные первого порядка:
 ,
,  ,
,
а затем частные производные второго порядка:

 ,
,  ,
,
 .
.
В примере 8 смешанные производные оказались тождественными, и это не случайно, так как имеет место следующая теорема.
Теорема 6 (о равенстве смешанных производных)
Если функция z = f(x, y) и ее частные производные f ¢ x , f ¢ y , f ¢ ¢ xy , f ¢ ¢ yx определены и непрерывны в точке Р(х, у) и в некоторой ее окрестности, то в этой точке справедливо равенство:
 (17)
(17)
Условие непрерывности частных производных является существенным: если оно не выполнено, то равенство (17) может оказаться неверным.
Производные второго порядка можно снова дифференцировать, как по х так и по у, в результате получим частные производные третьего порядка и т. д.
Таким образом, частной производной порядка n функции z = f(x, y) называется первая производная от частной производной (n–1 )-го порядка данной функции.
Для функции любого конечного числа переменных частные производные высших порядков определяются аналогично. Для них имеет место теорема о равенстве смешанных производных, т. е. о независимости результата от порядка дифференцирования, аналогичная теореме 6.
 и
и 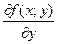 называют частными производными первого порядка. Их можно рассматривать как функции от
называют частными производными первого порядка. Их можно рассматривать как функции от  . Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом: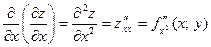 ;
;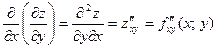 ;
; ;
; .
.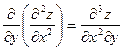 ,
, 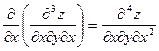 и т.д.
и т.д.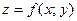 имеем:
имеем:  .
. | 7515 —
| 7515 —  или читать все.
или читать все.  ,
,  .
.  ,
,  .
.  ,
,  ,
,
 ,
,  ,
, .
. (17)
(17) 

