Найти базис и размерность линейной оболочки векторов
Пример1)
Найти базис и размерность линейной оболочки векторов a1=(1, 2, 3, 4), a2=( -1, 3, 2, 1),
a3=(- 1, 8, 7, 6), a4=(1, 4, -2, 5).
По определению базис максимальный набор линейно независимых векторов.
А) проверим, что вектора < a1, a2,a3, a4>–линейно независимы?
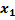 *a1+
*a1+  *a2+
*a2+ 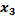 *a3+
*a3+  *a4=0
*a4=0
 =
= 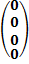

С помощью элементарных преобразований приводим матрицу к треугольному виду:

Выписываем решение….. Получаем, что вектора линейно зависимы значит вектора < a1, a2,a3, a4>не базис.
В) Из набор вектора < a1, a2,a3, a4>уберем один вектор, например a3.Проверим, что вектора < a1, a2, a4>образуют базис.
Дата добавления: 2015-09-07 ; просмотров: 3297 . Нарушение авторских прав
Базис и размерность

Размерность — количество векторов в базисе
Теорема о размерности суммы двух пространств
Теорема о ранге матрицы

Теорема о размерности пространства решений СЛАУ
ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
Ядро и образ линейного отображения, теорема о связи их размерностей.

Теорема об изоморфности конечно мерных векторных пространств одинаковой размерности.
Два конечномерных векторных пространства над одним и тем же полем изоморфны тогда и только тогда, когда равны их размерности.
Матрица линейного отображения конечномерных векторных пространств

Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8945 —  | 7615 —
| 7615 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Сайт о разделе высшей математики — линейной алгебре
п.5. Вычисление ранга матрицы и нахождение базиса линейной оболочки ее системы строк (столбцов).
Для вычисления ранга матрицы часто применяют метод Гаусса приведения матрицы к ступенчатому виду. Метод Гаусса основан на элементарных преобразованиях строк матрицы, которые, как мы уже знаем, не изменяют ранга системы строк, а значит не изменяют и ранга матрицы.
Таким образом, ранг данной матрицы равен рангу получившейся после преобразований ступенчатой матрицы. В свою очередь, ранг ступенчатой матрицы легко вычисляется, так как легко увидеть ее максимальный ненулевой минор и его порядок.
Пример. Вычислить ранг матрицы  и найти базис и размерность линейной оболочки натянутой на ее столбцы.
и найти базис и размерность линейной оболочки натянутой на ее столбцы.
1-й шаг: умножим первую строку на 2 и прибавим ко второй строке:
 ;
;
2-й шаг: прибавим к третьей строке первую, умноженную на (–3):
 ;
;
3-й шаг: прибавим ко второй строке 3-ю, умноженную на (–1):
 ;
;
4-й шаг: умножаем вторую строку на (–3) и прибавляем к третьей строке:
 .
.
Ранг последней матрицы равен 3, так как в первых трех столбцах стоит ненулевой минор 3-го порядка
 , а миноров 4-го порядка не существует.
, а миноров 4-го порядка не существует.
Приведенные преобразования не изменяют величину определителя, построенного на первых трех столбцах матрицы А, поэтому он отличен от нуля и, следовательно, его столбцы линейно независимые и образуют максимальную линейно независимую подсистему системы столбцов матрицы А. Отсюда можно сделать вывод, что первые три столбца матрицы А образуют базис линейной оболочки натянутой на столбцы матрицы А, т.е.  и
и  .
.
Ответ:  ,
,  – базис линейной оболочки
– базис линейной оболочки  ,
,  .
.
Определение. Любой ненулевой минор матрицы А максимального порядка называют базисным минором матрицы А.
Из этого определения следует, что порядок базисного минора матрицы А равен рангу матрицы А.
Замечание. Максимальную линейно независимую подсистему системы строк матрицы, которая образует базис линейной оболочки системы строк матрицы, мы будем, для краткости, называть базисными строками матрицы. И то же самое для столбцов.
Из приведенного примера можно сделать вывод, что если, вычисляя ранг матрицы, мы не переставляем строки и столбцы матрицы, то найдя базисный минор матрицы и определив номера строк и столбцов на которых он построен, мы, тем самым, находим номера базисных строк и столбцов исходной матрицы.
Так в примере, базисный минор матрицы А построен на первых трех строках и первых трех столбцах, следовательно именно они и образуют базисы системы строк и столбцов матрицы А.


