Решение диф уравнений методом эйлера

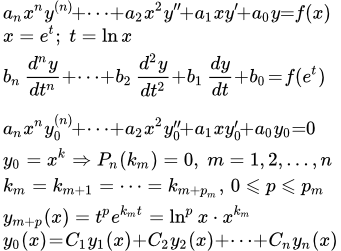
В более общем виде уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Если неоднородная часть имеет определенный вид, то получить общее решение проще, найдя частное решение неоднородного уравнения. К такому классу относятся уравнения вида:
(4)
,
где – многочлены от степеней и , соответственно.

Автор: Олег Одинцов . Опубликовано: 14-08-2013

В этом разделе приведены примеры решенных задач по теме численного решения обыкновенных дифференциальных уравнений (ОДУ) и систем. Разобраны наиболее известные методы Эйлера, Рунге-Кутта (разных порядков), приведено сравнение приближенных и точных решений, построены графики.

Решения задач на численное интегрирование дифференциальных уравнений онлайн

Задача 1.Численно решить задачу Коши для обыкновенного дифференциального уравнения 1-го порядка
на отрезке $[t_0, T]$ с шагом $h=0.2$ а) методом Эйлера; б) методом Рунге-Кутты 2-го порядка с оценкой погрешности по правилу Рунге.
Найти точное решение задачи. Построить на одном чертеже графики точного и приближенных решений.

Задача 2. Используя 1) метод Эйлера и 2) модифицированный метод Эйлера, найдите приближенное решение задачи Коши для обыкновенного дифференциального уравнения первого порядка $y’=f(x,y)$ удовлетворяющего начальным условиям $y(x_0)=y_0$ на отрезке $[a,b]$ с шагом $h=0.1$. Все вычисления вести с четырьмя десятичными знаками.

Задача 3. Численно решить задачу Коши для ОДУ 2-ого порядка методом Рунге-Кутта 4-го порядка. $$u»+e^x u’-(10+sin x )u+f=0, 0lt x lt 1$$ $$u(0)=0; u'(0)=50$$ $$f=50((11+sin x) sin x-e^x cos x). $$ Точное решение: $u=50 sin x, h=0.05, n=20$

Задача 4. Методом конечных разностей найти решение краевой задачи с шагами $h_1=(b-a)/5$, $h_2=(b-a)/10$ и оценить погрешность по правилу Рунге. Построить графики полученных приближенных решений.

КОБЕЦ Е.В.

ЛЕКЦИОННЫЙ МАТЕРИАЛ

ПО ДИСЦИПЛИНЕ «КОМПЬЮТЕРНОЕ

ОБЕСПЕЧЕНИЕ»

Решение обыкновенных дифференциальных уравнений. Метод Эйлера

Обыкновенные дифференциальные уравнения встречаются достаточно часто в различных прикладных задачах. Ими описываются задачи движения систем материальных точек, электрических цепей и др.

Дифференциальным называется такое уравнение, которое связывает независимую переменную Х, ее функцию y=f(x) и производные этой функции .

В неявном виде дифференциальное уравнение записывается так:

F(x, y, 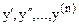)=0.

Порядок старшей производной, входящей в это уравнение, называется порядком дифференциального уравнения.

Если y=f(x) – функция одного независимого переменного Х, дифференциальное уравнение называется обыкновенным, если же y=f(x₁,x₂,…x_n) – функция n независимых переменных x₁,x₂,…x_n, то уравнение называется уравнением в частных производных.

Решение обыкновенного дифференциального уравнения сводится к поиску функции y=f(x), которая при подстановке в уравнение обращает его в тождество.

Поиск решения такого уравнения называется его интегрированием, а полученное решение – интегралом этого уравнения.

Существуют общее и частное решения дифференциального уравнения.

Общим решением уравнения 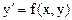является функция y=φ(x,c), удовлетворяющая уравнению при любых значениях постоянного С.

Частное решение определяется конкретным значением С. Для нахождения частного решения необходимо указать начальные условия, т.е. задать значения y, 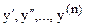при х=х, т.е. y=y(x), …,

Задача отыскания решения обыкновенного дифференциального уравнения при начальных условиях называется задачей Коши для обыкновенного дифференциального уравнения.

Мы рассматриваем уравнения разрешенными относительно старшей производной.

Их можно свести к системе n обыкновенных дифференциальных уравнений первого порядка заменой 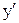на неизвестную функцию Р₁(х), 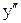на Р₂(х) и т.д., т.е.

1 производная 2 производная

Исходное уравнение в новом виде

Причем, начальные условия:

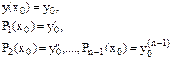
Для решения мы будем рассматривать методы Эйлера и Рунге-Кутта.

Численное решение состоит в построении таблицы приближенных значений y₁,y₂,…,y_n-1 точного решения y(x) уравнения .

Мы не знаем вида функции, не можем сразу вычислить значение функции. Знаем только начальные условия, значения Х=а, y=y(x) и интервал [a,b], на котором необходимо проинтегрировать функцию.

Задача ставится так: в точках Х,X₁,…,Х_n нужно найти приближения y,y₁,…,y_n точного решения.

Первый шаг – разбиваем отрезок на конечное число узловых точек (узлы сетки). Шаг сетки h=(b-a)/n, X_i=a+ih, I=0,1. N.

Нужно восстановить значения искомой функции. Рассмотрим дифференциальное уравнение 1 порядка

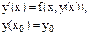
Второй шаг – зная начальные условия вычисляем значение первой производной в точке Х.

Третий шаг – в следующем узле сетки вычисляем значение функции.

На четвертом шаге все повторяется.

Геометрическая интерпритация метода состоит в замене интегральной кривой на отрезке касательной к ней в точке x_i,y_i. На каждом шаге заново определяется касательная, и, следовательно, соответствующая приближенному решению кривая будет ломаной линией. Поэтому метод называют еще методом ломаных.

Схема вычислений: x_i=a+ih (I=0,1,…,N)

Т.е. имея известную точку, вычисляем следующую. Это схема вычислений для уравнения 1 порядка.

Метод Эйлера для уравнений 2 порядка надо уравнение 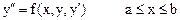с начальными условиями свести к системе 2 уравнений 1-го порядка:

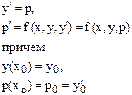
Производные берутся в точке х.

Итерационная формула вычислений:

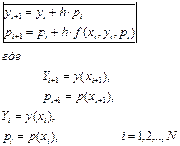
На практике вычисления проводятся снизу вверх: вначале вычисляется 1 производную, т.е. p_i, а затем вторую Y_i.

Для уравнения второго порядка приходится дважды применять интегрирование. Восстанавливаем значение производной, а затем значение искомой функции, т.е. решаем вначале одно уравнение, а затем второе.

Пример. На отрезке [a,b] составить таблицу значений приближенного решения дифференциального уравнения 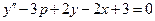, удовлетворяющего начальным условиям

Y(0)=1, Y΄(0)=2. шаг интегрирования h=0,2, точность ε=0,001. Предусмотреть печать значений точного решения y=e x +x.

Нужен массив Х – значений Х от 0 до 2

У – массив приближенных решений

Р – массив значений производной

(a-b)/h+ начальная точка = 2/0,2=10+1=11

Рассмотренный метод Эйлера относится к группе одношаговых методов, в которых для расчета точки (x_i+1, y_i+1) требуется информация о последней вычислительной точке (x_i, y_i).

Численное решение состоит в построении таблицы приближенных значений y₁, y₂, y₃, …,y_n-1 точного решения y(x) уравнения y¢=f(x,y), a£x£b при начальном условии y(x)=y, x=a на выбранной последовательности точек x_i=x+ih. Функция y зависит от аргумента х

нет

Точность метода или ошибкой обрыва называют ошибку, которую делают при переходе от предыдущего к последующему Х, если заменяют дифференциальное уравнение конечностным выражением.

Погрешность аппроксимации разностными уравнениями равна величине отброшенного остаточного члена ряда Тейлора O(h p +1 ).

Принято считать, если расчетные формулы численного метода согласуются с разложением в ряд Тейлора до членов порядка h p , то число р называют порядком точности метода.

В методе Эйлера сравнение формулы вычисления с разложением в ряд Тейлора согласуется до первого порядка по h, т.е. метод имеет первый порядок точности с локальной погрешностью O(h 2 )

Для метода Эйлера погрешность равна h 2 .

10.2. ЧИСЛЕННЫЙ МЕТОД ПОСТРОЕНИЯ ГРАФИКОВ

При решении задач на ЭВМ важное значение имеет наглядность и удобство быстрого восприятия изучаемых явлений. После освоения средств графического режима Турбо Паскаля можно строить графики, а также получать различные геометрические фигуры. Какие бы изображения не выводились на экран, все они строятся из точек, группы которых в свою очередь образуют отрезки и кривые. Вывод точки осуществляется процедурой PutPixel(X, Y, Color), где Х и Y-координаты экрана, где будет расположена точка. Color — ее цвет.

Для построения графика функции необходимо осуществить следующие операции:

1) Табулирование функции;

2) Нахождение максимального и минимального значений функции;

3) Формирование и вывод графика на экран.

Рассмотрим применение графического режима на примере построения графика функции Y(x)= x з /(2(x+1)(x + 1)) в области изменения х Î [-5,-1)U(-1, 5] с шагом h, а также построения асимптоты, заданной выражением Y(x) = х/2 — 1.

Табулирование функции можно осуществить с помощью следующих операторов:

х := xStart;

h : = (xEnd — xStart) / (n — 1) ;

for i : = 1 to n do begin

y[ i ] :=F(x);

if y[ i ] a then

где а — уровень ограничения.

Для определения масштаба вычерчиваемого графика необходимо найти минимальное и максимальное значения элементов массива Y. Это достигается с помощью операторов

for i := 1 to n do begin

if y[ i ] > yMax then

SetColor (цвет) — определяет цвет символов и линий.

Для установки курсора в указанную координату используется процедура MoveTo, (X, Y), а для вычерчивания линии от текущей линии до указанной координаты — процедура LineTo (X, Y).

При работе с графическими изображениями необходимо использовать систему координат. В зависимости от выбранного графического режима устанавливается разрешающая способность экрана в 320х200, 640х480 или другое число точек (пикселей). Программным путем можно установить максимальное число пикселей в строке с помощью функции GetMaxX, а число строк— с помощью функции GetMaxY. Начало координат имеет значение (0, 0), центр экрана — (GetMaxX div 2, GetMaxY div 2), а правый нижний угол — (GetMaxX, GetMaxY). При выполнении графических операций всегда указывается, что должен делать курсор, однако сам курсор в графическом режиме невидимый.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8546 — | 7400 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно