Решение уравнений методом последовательных приближений

Правила ввода функции

2. Примеры
   ≡ x^2/(1+x)
   cos 2 (2x+π) ≡ (cos(2*x+pi))^2
   ≡ x+(x-1)^(2/3)

На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).

Достаточные условия сходимости метода итерации

Процесс нахождения нулей функции методом итераций состоит из следующих этапов:

1. Получить шаблон с омощью этого сервиса.
2. Уточнить интервалы в ячейках B2 , B3 .
3. Копировать строки итераций до требуемой точности (столбец D ).

Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .

Метод последовательных приближений применяется для решения уравнений илисистем уравнений в случаях, когда искомые параметры не могут быть выражены в явном виде. В общем случае будем пред­полагать, чтоимеется некоторая функцияF(x) и необходимо найти та­кие значения аргументах, для которых

Функция F(x) может иметь какой угодно вид, она может быть ал­гебраической или трансцендентной, единственное, что будем предпо­лагать — это ее дифференцируемость.

В общем случае функции, которыми оперируют в задачах систем­ных исследований, не имеют аналитических формул для своих корней. Поэтому приходится пользоваться приближенными методами нахожде­ния корней, которые в основном состоят из двух этапов:

нахождение приближенного значения корня;

уточнение приближенного значения до некоторой заданной сте­пениточности.

Приближенное значение корня уравнения F(x) = 0 часто бывает из­вестно из физических соображений. Если это значение неизвестно, его можно найти с помощью грубого анализа функции. В качестве рекомен­дации можно предложить следующий метод. Определяются два такие значениях, для которыхF(x) имеет противоположные знаки, т.е. опре­деляются такиеX t иX., для которых

На втором шаге в качестве приближения возьмем

Продолжая этот процесс дальше, в качестве п-то приближения прини­маем значение

Процедура повторяется до тех пор, пока не будет достигнута задан­ная точность решения уравнения. Правило остановки можно задать следующим образом: вычислительный процесс заканчивается, когда выполняется соотношение |х_п— х_п,1

Задавая вектор начального приближения (х°,х°), находим первые приближенные оценки:

Повторяем эту процедуру до тех пор, пока разность (|х"- хГ‘|,|х₂"-х₂"‘|)не попадает вє-окрестность. Иными словами, дол­жны совместно выполняться соотношения:

В [8] доказано, что наилучшая сходимость достигается в случае, когда параметр а вычисляется следующим образом:

Метод Ньютона-Рафсона. Метод основан на разложении функ­ции F(x) в окрестностиа

Произведем элементарные преобразования в данном уравнении, полу­чим

Заменим искомый параметр его первым приближением, получим

Далее организуем итеративный процесс

Если начальное приближение хвыбрано близко к корню уравнения

и если производная F’(x) для/= 1,2. не равна нулю, то последо­вательность, порожденная соотношением(12.3) сходится ка.

Задачи, в которых требуется вычислить интегралы, возникают на разных этапах решения задач системного анализа. Иногда удается найти аналитическую формулу, т.е. выразить неопределенный интеграл в виде комбинаций алгебраических и трансцендентных функций, после чего остается вычислить значение определенного интеграла, подставив в формулу пределы интегрирования.

В большинстве случаев не удается найти никакой аналитической формулы или же она получается настолько сложной, что вычислять интеграл с ее помощью труднее, чем другими способами. В таких си­туациях приходится применять различные методы численного интегри-

рования, которые основаны на том, что интеграл представляется в виде предела суммы площадей. Далее вычисляют эту сумму с достаточно высокой степеньюточности.

Рассмотрим постановку задачи. Пусть необходимо вычислить оп­ределенный интеграл

при условии, чтоаиЪконечныи/(х)является непрерывной функцией

во всем интервале а

Метод прямоугольников. Пусть интервал [а, Ьразбит на мно­жество подынтервалов [х., х.₊₁). Будем считать, что на рассматривае­мом подынтервале интегрируемая функция почти константа:f(x)

(х —х)/(Q, гдеС, —произвольная точка на рассматриваемом подынтервале. Если в качестве такой точки взять среднюю точку подынтервала, получим формулу

Далее, производя суммирование по всем подынтервалам, получим фор­мулу интегрирования по методу прямоугольников

где п— количество подынтервалов на отрезке интегрирования.

Метод трапеций. В отличие от метода прямоугольников, где пред­полагалось, что интегрируемая функция на каждом подынтервале близ­ка к константе, в методе трапеций принимается допущение, что функ­ция на каждом подынтервале может быть приближена линейной функ­цией. При таком предположении интеграл заменяется площадью тра­пеции с высотой (х.₊₁—х.)и основаниями/ (х.₊₁) и /(х). В результате получим формулу трапеций

На рис. 12.1 приведена иллюстрация рассмотренных методов ин­тегрирования путем замены определенного интеграла конечной суммой, а именно показано увеличенное представление элемента площади, ограни­ченной функцией/(jc), осьюхи прямымиX = X. их = х._+гПунктирной линией выделена трапеция, которой заменяется площадь под кривой ин­тегрирования. В центре отрезка тонкой прямой линией отмечена высо­та прямоугольника, которая используется в качестве сомножителя в методе прямоугольников.

Ошибка интегрирования методом трапеций. При интегриро­вании с использованием формулы (12.5) возникает ошибка, равная сум­ме площадей между кривойу= f(x) и хордами, соединяющими точкиу.=/(jc )иу= /(х._+|). Оценим ошибку, разлагая функциюу = f (х)в ряд Тейлора в точкахjc. иX₁ .Это разложение позволит получить урав­нение исходной кривой в виде, удобном для сравнения точного значе­ния интеграла с приближенным, вычисленным по формуле(12.5).

Рассмотрим разложение функции у= f(x) в ряд Тейлора в окрест­ности точкиjc = Jt, Предположим, что интегрируемая функция имеет

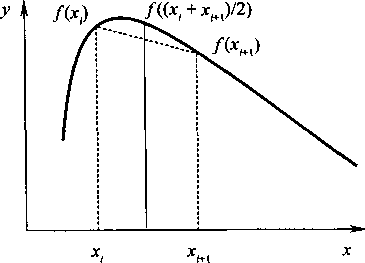
Рис. 12.1. Иллюстрация численного интегрирования методом трапеций

столько производных,сколько может потребоваться.

Аналогично разложим данную функцию в ряд в окрестности точки дс,получим

Обозначим длину подынтервала через А, т.е. A= дс _{Х ‘—fxi+},) + -. (12.8) Найдем среднее из обеих представлений(12.6) и(12.8)

Для малых h первый член гораздо больше всех остальных, поэтому ошибка именно им и определяется. Более того, в[8] показано, что за счет наличия в выражении слагаемых с производными более высокого порядка ошибка определяется следующим образом

Полную ошибку интегрирования методом трапеций можно оценить сле­дующим соотношением

Усовершенствованный метод трапеций. Попытаемся найти более точное значение интеграла. Для этого произведем сравнительно простое усовершенствование метода трапеций. Рассмотрим ошибку (12.11) и преобразуем данную формулу. На основании теоремы о сред­нем значении можно написать

Предположим теперь, что вторая производная от интегрируемой функции является константой, тогда и Сбудет константой.

Выберем другую величину шага разбиения отрезка интегрирования к = (Ь -а)/т,причемтФп.Тогда получим выражение для ошибки ин­тегрирования в виде

Запишем далее значение интеграла, вычисленное по правилу тра­пеций с шагом h -I_h и с шагомк — 1_к.Тогда будут справедливы следу­ющие выражения

Приравняем эти два уравнения друг другу и решим их относительно С, получим

Подставляя это выражение в (12.12), получим

Вычисленное таким образом значение интеграла является лучшим приближением, чем любое представление, полученное в (12.12). Если же вторая производная интегрируемой функции действительно посто­янна на интервале интегрирования[а, Ь],то ошибка в формуле(12.13) равна нулю.

Правило Симпсона. Способ интегрирования по правилу Симпсо­на наиболее широко известный и применяемый метод численного ин­тегрирования. В данном методе, так же как и в рассмотренных ранее, интегрирование производится путем разбиения общего интервала ин­тегрирования на множество более мелких отрезков. Однако в этом методе для вычисления площади над каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная па­рабола. Рассмотрим процедуру получения формулы Симпсона. Пусть, как н ранее, п —количество отрезков разбиения интервала интегриро­вания;h — ширина интервала разбиения. Предположим, что числоп является четным. Пустьк —ширина интервала при другом разбиении, такая, чток = 2А. Тоща можно записать

Преобразуем выражение (12.13) учитывая, чток = 2А, получим

Приведем подобные члены

Подставим данное выражение формулы (12.14) и(12.15), окончательно получим

Данная формула называется формулой Симпсона. Ошибка при интег­рировании с помощью формулы Симпсона равна

Как видно из данного выражения ошибка пропорциональна значе­нию А 4 ,в то время как для метода трапеций она была пропорциональнаА 2 .Это означает, что формула Симпсона соответствует ряду Тейлора с точностью до членов третьего порядка, а метод трапеций соответствует этому рядутолько сточностьюдо членов первого порядка. Поэтому при интегрировании многочленов степени не выше третьего порядка метод Симпсона дает точные значения интеграла.

Вычисление интегралов с бесконечными пределами. Рас­смотрим еще одну важную задачу численного интегрирования — вычис­ление определенного интеграла для случая, когда один или оба предела интегрирования равны бесконечности. Таким образом, предметом рас­смотрения будет вычисление одногоиз следующих выражений

Поскольку вычислительная техника не работает с такими понятия­ми как бесконечность, то задача аналитика состоит в том, чтобы за­менить бесконечность реальным числом, обеспечив приэтом прием­лемую точность вычисления. Иными словами, необходимо найти такие числаАиВ,для которых были бы справедливы выражения

Одной из целей этого метода состоит в нахождении приближенных решений уравнений. Одним из таких методов является метод простой итерации.

Метод простой итерации

Метод простой итерации — один из самых простейших численных методов для решения уравнений.

Идея метода простой итерации.

Пусть нам необходимо решить уравнение $fleft(x
ight)=0$.

Вначале для его решения приведем его к эквивалентному уравнению вида

Рассмотрим пример такого приведения:

Привести уравнение $-x^2=0$ к виду $x=varphi (x)$.

Решение.

Здесь есть три способа такого преобразования:

После этого каким-либо образом выбирается начальное приближение $x_0$, вычисляется значение $varphi (x_0)$ и находится уточненное значение $x_1=varphi (x_0)$. Следующее уточненное значение будет находиться как $x_2=varphi (x_1)$ и т.д. Каждый такой шаг называется шагом итерации.

Попробуй обратиться за помощью к преподавателям

Сформулируем и докажем следующую теорему:

Функция $varphi (x)$ определена и дифференцируема на отрезке $[a,b]$ и $varphi (x)in [a,b]$. Тогда, если extbar $<varphi >’left(x
ight)|

Процесс итерации $x_n=varphi (x_)$ сходится независимо от начального положения $x_0$;

$<mathop_ x_n >=X$ — единственный корень уравнения $x=varphi (x)$ на отрезке $[a,b]$.

Доказательство.

item Так как $X=varphi (x)$ и $x_n=varphi (x_)$, то

[x_n-X=varphi left(x_
ight)-varphi left(x
ight)=left(varphi left(x_
ight)-varphi left(x
ight)
ight)frac-x>-x>=] [=frac<varphi left(x_
ight)-varphi left(x
ight)>-x>cdot x_-x]

По теореме о среднем, получаем

Пусть $M=max |<varphi >’left(x
ight)|$, тогда $|x_n-X|le M|x_-x|$. Также$|x_-X|le M|x_-x|$. Но тогда получим

[left|x_n-X
ight|le Mleft|x_-x
ight|le M^2left|x_-x
ight|и т.д.]

То есть получим, что

Следовательно, для того чтобы метод сходился нужно, чтобы $M=max |<varphi >’left(x
ight)|$ было меньше единицы, значит $left|<varphi >’left(x
ight)
ight|

Рассмотрим $x_n=varphi (x_)$ и $x_=varphi (x_n)$.

[x_-x_n=varphi left(x_n
ight)-varphi (x_)]

По теореме о среднем $x_-x_n=f’left(x_n
ight)(x_n-x_)$.

Так как $left|<varphi >’left(x
ight)
ight|le q

Рассмотрим теперь $fleft(x
ight)=x-varphi left(x
ight)$, $f^<‘left(x
ight)>=1-<varphi >^<‘left(x
ight)>ge 1-q$. Значит, $left|x_n-varphi left(x_n
ight)
ight|=left|fleft(x_n
ight)-fleft(X
ight)
ight|=left|x_n-X
ight|left|f’left(x_n
ight)
ight|ge left(1-q
ight)|x_n-X|$. Следовательно, $|x_n-X|le frac<left|x_n-varphi left(x_n
ight)
ight|><1-q>le frac<|x_-x_n|><1-q>$.

Из двух полученных неравенств, имеем

Пусть $|x_n-X|le varepsilon $, тогда $x_0,x_1,dots ,x_n$ нужно вычислять до тех пор, пока не выполнится неравенство $|x_n-x_|le frac<varepsilon (1-q)>$, тогда получим, что $X=x_npm varepsilon $. Отсюда следует, что $X$ корень уравнения $x=varphi (x)$, то есть $X=varphi (X)$.

Предположим, что это уравнение имеет еще один корень $X’=varphi left(X’
ight)$. Отсюда $X’-X=varphi left(X’
ight)-varphi left(X
ight)$, тогда $left(X’-X
ight)left|1-<varphi >’left(C
ight)
ight|=0$. Значит $X’=X$.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Теорема доказана.

Из теоремы будет вытекать погрешность метода простой итерации. Она определяется следующей формулой:

Также из нее можно выделить критерий окончания метода простой итерации. Он говорит, что процесс итерации необходимо продолжать до выполнения следующего неравенства:

Рассмотрим теперь на примере использование метода простой итерации.

Решить уравнение $sinx-x^2=0$ с точностью до $varepsilon =0,001$.

Решение.

Вначале приведем уравнение к виду $x=varphi (x)$.

Очевидно, что корень уравнения находит на отрезке $left[frac<pi ><6>,frac<pi ><3>
ight]$.

Найдем $varphi (x)$:

Она возрастает на отрезке $left[frac<pi ><6>,frac<pi ><3>
ight]$, следовательно принимает максимальное значение, при $x=frac<pi ><3>$. $left|<varphi >’left(x
ight)
ight|le left|<varphi >’left(frac<pi ><3>
ight)
ight|approx 0,312$.

Условие выполняется, $q [|x_n-x_|le varepsilon ]

Это неравенство выполнится на 5 шаге.

Приведем таблицу промежуточных решений, взяв за $x_0$ единицу:

Ответ: приближенное значение с заданной точностью — $0,8765$.

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь