Метод прогонки (алгоритм Томаса) используют для решения СЛУ типа Ax=F, где A — трёхдиагональная матрица. Это вариант метода последовательного исключения неизвестных.
Система уравнений Ax=F равноценна соотношению:
Метод прогонки базируется на предположении, что неизвестные, которые необходимо найти, связаны соотношением:
Выразим xi-1 и xi через xi+1, подставим в уравнение, используя это соотношение, (1):
где Fi — правая часть i-го уравнения.
Это соотношение выполняется не завися от решения, если потребовать:
,
,
Получаем из 1-го уравнения:
.
После того, как нашли прогоночные коэффициенты α и β, используем уравнение (2) и получим решение системы. Причем,
.
Еще одним вариантом объяснения смысла метода прогонки является такой вариант: преобразуем уравнение (1) к равнозначному ему уравнению:
c надиагональной (наддиагональной) матрицей:
Рассчеты проводим в 2 этапа. На 1-ом этапе вычисляем компоненты матрицы C′i и вектора F′, начиная с i=2 до i=n:
На 2-ом этапе, для i=n,n−1,…,1 вычисляем решение:
Для применимости формул метода прогонки достаточно свойства строгого диагонального преобладания у матрицы A.
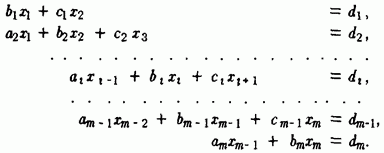
Преобразуем первое уравнение системы к виду 
Подставим полученное выражение во второе уравнение системы:
Преобразуем это уравнение к виду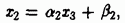 
Выражение подставляем в третье уравнение системы и т. д. Далее уравнение системы преобразуется к виду 
. На следующем шаге подстановка в последнее уравнение выражения дает
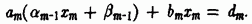
Отсюда можно определить значение
Уточнение решения системы линейных алгебраических уравнений.
Определение возможной ошибки решения системы линейных алгебраических уравнений.
Системы однородных линейных уравнений. Методы их решения.
Собственные значения и собственные векторы матриц.
Вектор 
, называетсясобственным вектором квадратной матрицы 
, если существует такое число 
, что 
. При этом число называетсясобственным значением матрицы , соответствующим собственному вектору 
. может быть записано в виде 
.Если — собственное значение матрицы , а соответствующий ему собственный вектор, то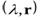 
называютсобственной парой матрицы .
Методы развёртывания векового уравнения.
1. метод Данилевского
Сущность метода заключается в приведении векового определителя к нормальному виду Фробениуса:
Метод Данилевского позволяет определить и собственные векторы с точностью до постоянного множителя.
2. метод Крылова
Характеристический полином вектора А:
= 0
Коэффициенты pj где j=1,2,3,…n характеристического полинома определяются из системы уравнений вида:
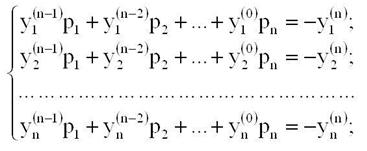
Коэффициенты вычисляются по формулам:
3. метод Леверрье
Основан на формулах Ньютона для сумм степеней корней алгебраического уравнения. Алгоритм метода:
1) вычисляются степени данной матрицы А
2) вычисляются суммы элементов главных диагоналей матриц
3) вычисляются коэффициенты характеристического полинома матрица А
Приближение функций. Понятие обобщённого полинома.
Данную функцию f(x) требуется заменить обобщенный полиномом Qm(x) заданного порядка «m» так, чтобы отклонение функции f(x) от обобщенного полинома Qm(x) на указанном множестве X=, x1,…, xn> было наименьшим.
Обобщенный полином Qm(x) имеет вид:
Интерполирование функций.
Точечное квадратичное аппроксимирование функций.
Понятие о равномерном приближении функций.
Понятие о среднеквадратичном отклонении функций на множестве параметрических точек.
Введем соответствующее расстояние 
между данной непрерывной функцией f(х) и непрерывным аппроксимирующим обобщенным полиномом Q(x), так называемое среднее квадратичное отклонение.Абсолютным отклонением на [а, b] обобщенного полинома Qm (x) от данной непрерывной функции f(х) называется число
Если 
, то из формулы следует 
для всех точек х на отрезке [а, b].
Приближённое вычисление интегралов. Формула прямоугольников.
приближенное значение интеграла с избытком
приближенное значение интеграла с недостатком
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Система уравнений для определения коэффициентов сплайна представляет собой частный случай систем линейных алгебраических уравнений
с трехдиагональной матрицей , т.е. с матрицей, все элементы которой,не лежащие на главной и двух побочных диагоналях, равны нулю при та
В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид
Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных.
Т.е. матрицу А можно записать
Идея метода прогонки состоит в следующем. Решение системы (1) ищется в виде
где — неизвестные коэффициенты, которые последовательно находятся от до (прямая прогонка), а затем последовательно вычисляются (обратная прогонка) .
Выведем формулы для вычисления Из (3) можно получить
Подставляя имеющиеся выражения для в уравнение (1), приходим при к уравнению Последнее уравнение будет выполнено если коэффициенты выбрать такими, чтобы выражения в квадратных скобках обращались в нуль.
А именно, достаточно положить
Для отыскания всех достаточно задать
Эти начальные значения находим из требования эквивалентности условия (3) при т.е. условия , первому из уравнений (2).
Таким образом, получаем
Нахождение коэффициентов по формулам (4), (5) называется прямой прогонкой. После того, как прогоночные коэффициенты найдены, решение системи (1), (2) находится по рекуррентной формуле (3), начиная с Для начала счета по этой формуле требуется знать , которое определяется из уравнений
Нахождение по формулам
называется обратной прогонкой.
Алгоритм решения системы (1), (2) определяемый формулами (4)-(6) называется методом прогонки.
Метод прогонки можно пременять, если знаменатели выражений (4), (6) не обрщаются в нуль.
Покажем, что для возможности применения метод прогонки достаточно потребовать, чтобы коэффициенты системы (1), (2) удовлетворяли условиям
Сначала докажем по индукции, что при условиях (7), (8) модули прогоночных коэффициентов не превосходят единицы. Согласно (5), (8) имеем . Предположим, что для некоторого и докажем, что
Прежде всего для любых двух комплексных чисел и докажем неравенство
Из неравенства треугольника имеем
Вернемся теперь к доказательству , если . Согласно имеем оценку
а, используя (7) , получаем
т.е. знаменатели выражений (4) не обращаются в нуль.
Далее, учитывая второе из условий (8) и только что доказанное неравенство , имеем
т.е. не обращается в нуль и знаменатель в выражении для .
К аналогичному выводу можно прийти и в том случае, когда условия (7), (8) заменяются условиями
Таким образом при выполнении условий (7), (8) (так же как и условий (9), (10)) система (1), (2) эквивалентна системе (4)-(6). Поэтому эти условия гарантируют существование и единственность решения системы (1), (2) и возможность нахождения этого решения методом прогонки.
Кроме того, доказанные неравенства , обеспечивают устойчивость счета по рекуррентным формулам (6). Последнее означает, что погрешность,внесенная на каком-либо шаге вычислений, не будет возрастать при переходе к следующим шагам.
Действительно, пусть в формуле (6) при вместо вычислена величина
Тогда на следующем шаге вычислений, т.е. при
получим величину и погрешность окажется равной
Отсюда получаем, что ,т.е. погрешность не возрастает.
Подсчитаем число арифметических действий, выполняемых при решении задачи (1), (2) методом прогонки.
По формулам (4), что реализуемые с помощью шести арифметических действий, вычисления производятся раз, по формуле (6) выполняется 5 арифметических действий, наконец по формуле (3), требующей всего два действия, вычисления осуществляются раз. Итак в методе прогонки всего затрачивается
арифметических действий, т.е. число действий растет линейно относительно числа неизвестных
При решении же произвольной системы линейных алгебраических уравнений методом Гаусcа число действий пропорционально кубу числа неизвестных.
Загрузка...
