Содержание
Симметрической разностью множеств А и В называют множество, состоящее из объединения множеств разностей АВ и ВА. Симметрическая разность множеств А и В обозначается символом D (или символом Å). Таким образом, по определению
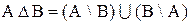. 1.17
Нетрудно убедиться, что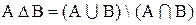 
. 1.18
Примеры.
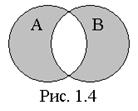
Графически симметричная разность множеств А и В может быть представлена как показано на рис. 1.4. Закрашенные области соответствуют симметрической разности множеств А и В.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8914 — 
| 7222 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Симметрическую разность можно описать двумя способами:
симметрическая разность двух заданных множеств A и B — это такое множество A Δ B, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество: А Δ В = (А В) ∪ (В А)
Например, если А=<1,2,3,4>, B=<3,4,5,6>, то А Δ В = (А В) ∪ (В А) = <1,2>∪ <5,6>=
симметрическая разность двух заданных множеств A и B — это такое множество A Δ B, куда входят все те элементы обоих множеств, которые не являются общими для двух заданных множеств. А Δ В = (A ∪ B) (A ∩ B)
Онлайн калькулятор позволяет найти симметрическую разность множеств A и B (А Δ B).
Также доступны следующие операции над множествами: объединение, пересечение, разность.
Операции на множествах. Свойства операций
Операции на множествах
1. Объединение
Объединение двух множеств:
Пусть даны два множества и тогда их объединением называется множество содержащее в себе все элементы
исходных множеств:
Объединение более чем двух множеств:
Пусть дано семейство множеств тогда его объединением называется множество, состоящее из всех элементов всех множеств семейства:
Пересечение
Пусть даны два множества и , тогда их пересечением называется множество , которому принадлежат те и только те элементы, которые одновременно принадлежат двум множествам:
3.Разность
Пусть даны два множества и , тогда их разностью называется множество , содержащее в себе элементы , но не :
4.Симметрическая разность
Пусть даны два множества и тогда их симметрической разностью называется множество , куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество:
5.Дополнение
Пусть дано множество его дополнением называется семейство элементов, не принадлежащие данному множеству:
Свойства операций
Пусть — произвольные множества, тогда:
1. Операция объединение множеств коммутативна:
2. Операция объединение множеств ассоциативна:
3. Операция пересечение множеств коммутативна:
4. Операция пересечения множеств ассоциативна:
Загрузка...
