Симплекс метод пример решения задачи

Классификацию решения задач линейного программирования можно представить в виде следующей схемы.

Метод решения	Примечание	Целевая функция
1. Графический метод	Используется при двух переменных (x1, x2)	max, min
2. Симплексный метод	Формы записи: симплексная таблица, строчечная форма, строковая форма. Алгоритм решения: метод искусственного базиса (М-метод, двухфазный метод), правило прямоугольника, правило Креко	max, min
3. Двойственный симплекс-метод	Формы записи: симплексная таблица, строчечная форма, строковая форма. Алгоритм решения: метод искусственного базиса (М-метод, двухфазный метод)	min
4. Двойственная задача	Алгоритм решения: симплекс-метод, теоремы двойственности	max, min
5. Метод Гомори	Алгоритм решения: метод отсечений	max, min

Ниже представлены примеры решения задач линейного программирования.

Линейное программирование. Решение задач графическим способом

Симплексный метод решения задач линейного программирования

1. Метод искусственного базиса
2. Задача оптимального производства продукции
3. Пример решения симлекс-методом
   Решить следующую задачу ЛП в неканонической форме симплекс-методом:
   f(x) = x₁ – x₂ – 3x₃ → min
4. М-метод. Решить задачу М-задачу.
5. Пример нахождения максимума функции симплексным методом
6. Пример нахождения минимума функции симплексным методом
7. Пример решения модифицированным симплекс-методом
8. Пример решения симплекс-методом в столбцовой форме записи
9. Симплекс-метод в строчечной форме записи. Пример решения
10. Пример решения задачи симплексным методом в Excel
11. Линейное программирование в Excel

Решение двойственной задачи линейного программирования

1. Двойственная задача ЛП
   Необходимо выполнить в указанном порядке следующие задания.
   1. Найти оптимальный план прямой задачи:
   а) графическим методом;
   б) симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса).
   2. Построить двойственную задачу.
   3. Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
2. Двойственная задача в Excel
3. Оценка целесообразности выпуска новой продукции

Двойственный симплекс-метод

1. Алгоритм двойственного симплекс-метода. Подробный пример решения Р-методом

Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, последовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность, когда в результате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, математическая логика, совмещаются с логически обоснованным пониманием сущности изучаемого явления.

Методом линейного программирования решается транспортная задача, т.е. задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.

Если вы уже разобрались с графическим методом решения задач линейного программирования, самое время переходить к симплекс-методу. В отличие от первого, он практически не имеет ограничений на задачу (любое количество переменных, разные знаки и т.п.) и модифицируется в зависимости от типа задачи (например, М-метод или метод искусственного базиса).

При решении задачи симплекс методом вычисления обычно ведутся (для компактности и наглядности) в таблицах (табличный симплекс-метод), причем последняя таблица с оптимальным решением содержит важную дополнительную информацию: решение двойственной задачи, остатки ресурсов, сведения о дефицитных ресурсах и т.п., которая позволяет провести экономический анализ задачи линейного программирования (см. ниже пример 3).

Примеры решений задач симплекс-методом выложены бесплатно для вашего удобства — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий, перейдите в раздел: решение линейного программирования на заказ.

Решение задач симплекс-методом: примеры онлайн

Задача 1. Компания производит полки для ванных комнат двух размеров — А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В — 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В — 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В — 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?

Задача 2. Решить задачу линейного программирования симплекс-методом.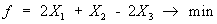

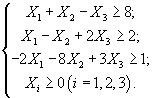
Задача 3. Предприятие производит 3 вида продукции: А1, А2, А3, используя сырьё двух типов. Известны затраты сырья каждого типа на единицу продукции, запасы сырья на планируемый период, а также прибыль от единицы продукции каждого вида.

Сырьё	Затраты сырья на единицу продукции			Запас сырья
А1	А2	А3
I	3,5	7	4,2	1400
II	4	5	8	2000
Прибыль от ед. прод.	1	3	3

1. Сколько изделий каждого вида необходимо произвести, чтобы получить максимум прибыли?
2. Определить статус каждого вида сырья и его удельную ценность.
3. Определить максимальный интервал изменения запасов каждого вида сырья, в пределах которого структура оптимального плана, т.е. номенклатура выпуска, не изменится.
4. Определить количество выпускаемой продукции и прибыль от выпуска при увеличении запаса одного из дефицитных видов сырья до максимально возможной (в пределах данной номенклатуры выпуска) величины.
5. Определить интервалы изменения прибыли от единицы продукции каждого вида, при которых полученный оптимальный план не изменится.

Задача 4. Решить задачу линейного программирования симплексным методом:

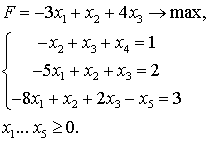
Задача 5. Решить задачу линейного программирования симплекс-методом: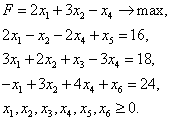

Задача 6. Решить задачу симплекс-методом, рассматривая в качестве начального опорного плана, план, приведенный в условии: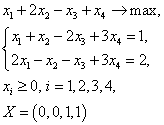

Задача 7. Решить задачу модифицированным симплекс-методом.
Для производства двух видов изделий А и Б используется три типа технологического оборудования. На производство единицы изделия А оборудование первого типа используется а1=4 часов, оборудование второго типа а2=8 часов, а оборудование третьего типа а3=9 часов. На производство единицы изделия Б оборудование первого типа используется б1=7 часов, оборудование второго типа б2=3 часов, а оборудование третьего типа б3=5 часов.
На изготовление этих изделий оборудование первого типа может работать не более чем t1=49 часов, оборудование второго типа не более чем t2=51 часов, оборудование третьего типа не более чем t3=45 часов.
Прибыль от реализации единицы готового изделия А составляет АЛЬФА=6 рублей, а изделия Б – БЕТТА=5 рублей.
Составить план производства изделий А и Б, обеспечивающий максимальную прибыль от их реализации.

Задача 8. Найти оптимальное решение двойственным симплекс-методом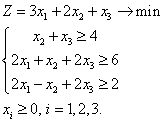

Условие задачи

Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве b₁ = 240, b₂ = 200, b₃ = 160 единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве a₁₁ = 2 единицы, ресурса второго вида в количестве a₂₁ = 4 единицы, ресурса третьего вида в количестве a₃₁ = 4 единицы. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве a₁₂ = 3, a₁₃ = 6 единицы, ресурса второго вида в количестве a₂₂ = 2, a₂₃ = 4 единицы, ресурса третьего вида в количестве a₃₂ = 6, a₃₃ = 8 единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно c₁ = 4, c₂ = 5, c₃ = 4 (тыс. руб.). Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.

К прямой задаче планирования товарооборота, решаемой симплекс методом, составить двойственную задачу линейного программирования.
Установить сопряженные пары переменных прямой и двойственной задачи.
Согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров.

Решение задачи симплекс методом

= 0>>><

Решаем симплекс методом.

Вводим дополнительные переменные x₄ ≥ 0, x₅ ≥ 0, x₆ ≥ 0, чтобы неравенства преобразовать в равенства.

Данные заносим в симплекс таблицу

Симплекс таблица № 1

0 · 240 + 0 · 200 + 0 · 160 = 0

Вычисляем оценки по формуле:

Δ₁ = 0 · 2 + 0 · 4 + 0 · 4 – 4 = – 4
Δ₂ = 0 · 3 + 0 · 2 + 0 · 6 – 5 = – 5
Δ₃ = 0 · 6 + 0 · 4 + 0 · 8 – 4 = – 4
Δ₄ = 0 · 1 + 0 · 0 + 0 · 0 – 0 = 0
Δ₅ = 0 · 0 + 0 · 1 + 0 · 0 – 0 = 0
Δ₆ = 0 · 0 + 0 · 0 + 0 · 1 – 0 = 0

Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:

Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₂.

= 26.667

Наименьшее неотрицательное: Q₃ = 26.667. Выводим переменную x₆ из базиса

3-ю строку делим на 6.
Из 1-й строки вычитаем 3-ю строку, умноженную на 3
Из 2-й строки вычитаем 3-ю строку, умноженную на 2

Получаем новую таблицу:

Симплекс таблица № 2

0 · 160 + 0 · 440/3 + 5 · 80/3 = 400/3

Вычисляем оценки по формуле:

Δ₁ = 0 · 0 + 0 · 8/3 + 5 · 2/3 – 4 = – 2/3
Δ₂ = 0 · 0 + 0 · 0 + 5 · 1 – 5 = 0
Δ₃ = 0 · 2 + 0 · 4/3 + 5 · 4/3 – 4 = 8/3
Δ₄ = 0 · 1 + 0 · 0 + 5 · 0 – 0 = 0
Δ₅ = 0 · 0 + 0 · 1 + 5 · 0 – 0 = 0
Δ₆ = 0 · (–1)/2 + 0 · (–1)/3 + 5 · 1/6 – 0 = 5/6

Поскольку есть отрицательная оценка Δ₁ = – 2/3, то план не оптимален.

Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₁.

Наименьшее неотрицательное: Q₃ = 40. Выводим переменную x₂ из базиса

3-ю строку делим на 2/3.
Из 2-й строки вычитаем 3-ю строку, умноженную на 8/3

Получаем новую таблицу:

Симплекс таблица № 3

0 · 160 + 0 · 40 + 4 · 40 = 160

Вычисляем оценки по формуле:

Δ₁ = 0 · 0 + 0 · 0 + 4 · 1 – 4 = 0
Δ₂ = 0 · 0 + 0 · (–4) + 4 · 3/2 – 5 = 1
Δ₃ = 0 · 2 + 0 · (–4) + 4 · 2 – 4 = 4
Δ₄ = 0 · 1 + 0 · 0 + 4 · 0 – 0 = 0
Δ₅ = 0 · 0 + 0 · 1 + 4 · 0 – 0 = 0
Δ₆ = 0 · (–1)/2 + 0 · (–1) + 4 · 1/4 – 0 = 1

Поскольку отрицательных оценок нет, то план оптимален.

То есть необходимо реализовать товар первого вида в объеме 40 тыс. руб. Товар 2-го и 3-го видов реализовывать не надо. При этом максимальная прибыль составит F_max = 160 тыс. руб.

Решение двойственной задачи

Двойственная задача имеет вид:

=4> <3y_1 + 2y_2 + 6y_3>=5> <6y_1 + 4y_2 + 8y_3>=4> = 0>>><

Вводим дополнительные переменные y₄ ≥ 0, y₅ ≥ 0, y₆ ≥ 0, чтобы неравенства преобразовать в равенства.

Сопряженные пары переменных прямой и двойственной задач имеют вид:

Основные	Дополнительные
x1	x2	x3	x4	x5	x6
y4	y5	y6	y1	y2	y3
Дополнительные	Основные

Из последней симплекс таблицы № 3 прямой задачи, находим решение двойственной задачи:

Автор: Олег Одинцов . Опубликовано: 08-12-2011