Синус угла в паскале

Функция Sin Pascal-Паскаль

• Скачено бесплатно: 7747
• Куплено: 414

• Pascal-Паскаль->S->Функция Sin Pascal-Паскаль

Описание

Sin: Возвращает синус параметра.

Замечания:

X — выражение вещественного типа. Возвращает синус угла X в радианах.

Пример программы для функции Sin

• ArcTan
• TypeOf
• Cos

Программирование

Исходники Pascal (127)

Справочник

Справочник по паскалю: директивы, функции, процедуры, операторы и модули по алфавиту

Тригонометрические функции Cos и Sin в Паскале вычисляют соответственно косинус угла и синус угла. Можете сразу перейти к просмотру видео, где я рассказал об этих функциях. Но также рекомендую прочитать статью — не вся информация вошла в видеоролик.

На всякий случай (для тех, кто подзабыл математику) я расскажу, что такое косинус (Cos) и синус (Sin) угла. Но позже — в конце статьи. А сейчас синтаксис в Паскале и некоторые особенности работы с этими функциями.

Синтаксис функции Cos:

function Cos(Х : ValReal) : ValReal;

Синтаксис функции Sin:

function Sin(Х : ValReal) : ValReal;

О типе ValReal я рассказывал здесь.

Функция Cos возвращает косинус угла Х. Функция Sin возвращает синус угла Х. Значение угла передаётся через параметр Х и выражается в радианах.

ВНИМАНИЕ! Не в градусах, а в радианах!

Так как мы больше привыкли измерять углы в градусах, то, если мы не хотим попрощаться с этой привычкой, нам придётся переводить градусы в радианы.

Формула перевода градусов в радианы проста:

Радиан := Пи * Градус / 180

Как известно, число ПИ равно 3,14 (примерно). Можно использовать непосредственно число для преобразования градусов в радианы.

Однако удобнее использовать предопределённую константу Pi, как это сделано в примере ниже.

Здесь мы объявляем три переменных. Затем просим пользователя ввести угол в градусах и читаем введённое значение в переменную z.

Затем преобразуем градусы в радианы и сохраняем полученный результат в переменную у.

Ну а затем уже используем функции Cos и Sin для получения нужных нам косинуса и синуса для угла, указанного пользователем.

А напоследок выводим значение числа ПИ, которое берём из предопределённой в Паскале константы Pi.

Ну а теперь пришло время выполнить своё обещание, то есть рассказать подробнее о косинусах и синусах.

Что такое косинус и синус угла

Для начала внимательно посмотрите на рисунок.

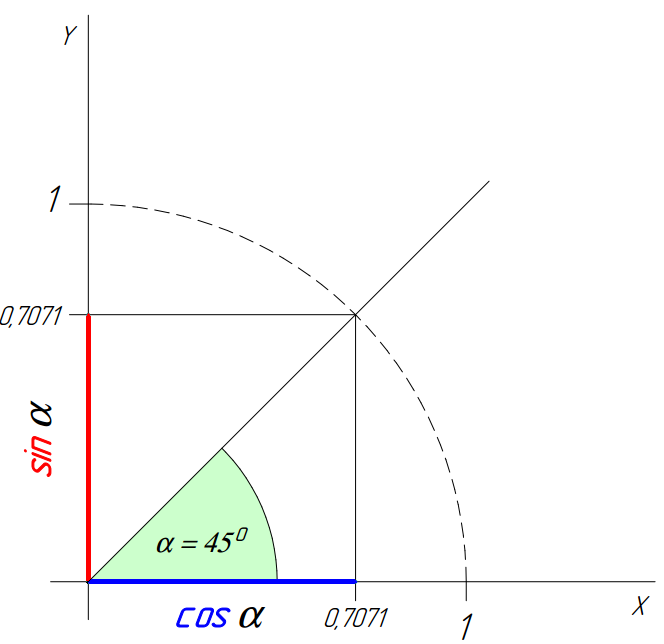
Как видно из рисунка, величина тригонометрических функций зависит от угла между осью Х и прямой, проведенной из центра координат.

На рисунке угол равен 45 градусам. При таком значении угла синус равен косинусу (0,7071).

Если угол равен 0 градусов (прямая совпадает с осью Х), то косинус равен 1, а синус равен 0. Если угол равен 90 градусов (прямая совпадает с осью Y), то косинус равен 0, а синус равен 1.

В любом случае значения этих функций лежат в пределах от –1 до +1 включительно. Например, синус 30 градусов равен 0,5. В этом случае значение 0,5 – это так называемая обратная функция. Если необходимо указать, что функция является обратной, то к названию функции добавляют приставку arc. Пример (в функции cos угол указан в градусах):

Остальные тригонометрические функции – это выражения, содержащие синус и/или косинус:

И хотя в Паскале есть функции для вычисления других тригонометрических функций, вы можете вполне обойтись без них, используя приведённые выше формулы.

И теперь у вас достаточно знаний, чтобы написать какую-нибудь свою полезную программку для вычисления тригонометрических функций. Это требуется очень часто студентам, школьникам и инженерам.

Мы уже знаем, какие существуют функции для целых переменных. Это – нахождение модуля числа (Функция Abc), а также возведение числа в квадрат (Функция Sqr). В этом уроке мы рассмотрим функции, применяемые к дробным числам. Это функции Sqr — квадрат числа, Abs — модуль числа, Sqrt — корень числа, а также известные всем математические функции Sin, Cos, Arctan, Ln, Exp, Pi.

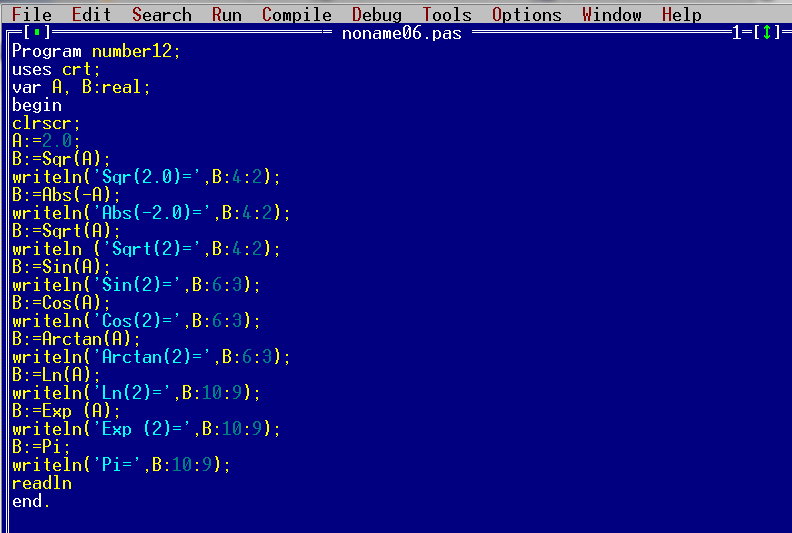
В строке №7 записывается функция Sqr. Это функция возведения числа в квадрат.

В строке №9 записывается операция нахождения модуля числа.
Функции Sqr и Abs мы разбирали в уроке Abs, Sqr в Pascal.

В строке №11 записывается функция Sqrt. Данная функция подсчитывает корень числа, стоящего в скобках после слова Sqrt. В нашем случае функция Sqrt будет считать корень из числа «2».

В строке №13 записываем функцию Sin. Данная функция будет подсчитывать синус числа, стоящего в скобках после записи функции.

Строка №15. Функция Cos подсчитывает косинус числа, стоящего в скобках после функции.

Строка №17. Функция Arctan вычисляет арктангенс числа, стоящего в скобках после записи функции.

Строка №19. Функция Ln подсчитывает логарифм числа, стоящего в скобках после записи функции.

Строка №21. Функция Exp возводит число «e» (экспонента — 2.72. ) в степень, значение которой указывается в скобках после слова Exp. Т.е. в нашем случае число «e» будет возведено в степень «2».

Строка №23. Переменной «B» будет присвоено значение числа «?».

Дополнение к материалу.

• Функции Sqrt, Sin, Cos, Arctan, Ln, Exp, Pi определены только для вещественных (дробных) чисел.
• В Паскале не существует операции возведения в степень. Есть только операция возведения числа в квадрат (Sqr). Чтобы возвести число в степень используют операцию умножения. Например, чтобы возвести число 3 в 5-ю степень необходимо записать 3*3*3*3*3