С тем, чтобы проиллюстрировать применение законов динамики твёрдого тела, решим задачу о скатывании цилиндра с наклонной плоскости (рис. 10.5).
Сплошной цилиндр массы m и радиуса R скатывается без проскальзывания с наклонной плоскости. Угол наклона плоскости — a, а высота Н (Н » R). Начальная скорость цилиндра равна нулю. Определим время скатывания — Т и скорость центра масс цилиндра у основания наклонной плоскости.
При качении цилиндра на него действуют три силы: сила тяжести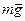 
, упругая сила реакции опоры 
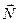и сила трения покоя 
(ведь качение без проскальзывания!).
Представим это движение суммой двух движений: поступательного со скоростью VC, с которой движется ось цилиндра, и вращательного вокруг оси цилиндра с угловой скоростью w.
. (10.9)
Эта связь скоростей поступательного и вращательного движений следует из условия «движение без проскальзывания».
Продифференцировав уравнение (10.9) по времени, получим соотношение углового и линейного ускорений цилиндра:
, то есть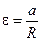 
.
Воспользовавшись теоремой о движении точки центра масс, опишем поступательное движение цилиндра:
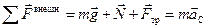. (10.10)
Для описания вращения воспользуемся основным уравнением динамики вращательного движения:
Спроецировав уравнение (10.10) на направления осей x и y, получим два скалярных уравнения:
Обратимся теперь к уравнению (10.11). Из трёх названных сил момент относительно оси цилиндра создаёт только сила трения:
.
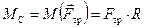Момент инерции сплошного цилиндра относительно его оси равен (см. лекцию №9):
.
Учитывая всё это, уравнение (10.11) перепишем так:
. (10.14)
Решая совместно уравнения (10.12) и (10.14), получим следующие значения неизвестных величин:
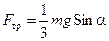; (10.15)
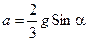. (10.16)
Из уравнения (10.15) следует, что с увеличением угла наклона a должна возрастать и сила трения покоя Fтр. Но, как известно, её рост ограничен предельным значением:
. (10.17)
Так как сила трения покоя (10.15) не может превышать предельного значения (10.17), то должно выполняться неравенство:
Отсюда следует, что скатывание будет происходить без проскальзывания до тех пор, пока угол a не превзойдёт значения aпред:
Здесь m — коэффициент трения цилиндра по плоскости.
Линейное ускорение цилиндра (10.16) величина неизменная, следовательно, поступательное движение цилиндра равноускоренное. При таком движении без начальной скорости цилиндр достигнет основания наклонной плоскости за время:
.
Здесь: l = 
— длина плоскости;
a =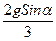
, (см.10.16).
Значит, время скатывания:
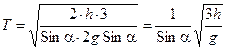. (10.18)
Вычислим конечную скорость поступательного движения оси цилиндра:
. (10.19)
Заметим, что эту задачу можно решить проще, воспользовавшись законом сохранения механической энергии.
В системе, правда, присутствует сила трения, но её работа равна нулю, поскольку точка приложения этой силы в процессе спуска остаётся неподвижной: ведь движение происходит без проскальзывания. Раз нет работы силы трения, механическая энергия системы не меняется.
Рассмотрим энергию цилиндра в начальный момент — на высоте h и в конце спуска. Полная энергия цилиндра в этих положениях одинакова:
.
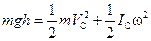Вспомним, что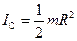 
и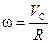 
. Тогда уравнение закона сохранения энергии можно переписать так:
.
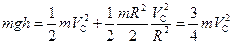Отсюда легко найдём конечную скорость цилиндра:
,
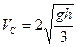которая блестяще подтверждает полученный нами ранее результат (10.19).
Лекция 11 «Элементы механики жидкости»
1. Давление жидкости. Законы гидростатики.
2. Стационарное течение жидкости. Уравнение неразрывности потока.
3. Основной закон динамики для идеальной жидкости. Уравнение Бернулли.
4. Применение уравнения Бернулли для решения задач гидродинамики.
4.1. Истечение жидкости из сосуда.
4.2. Манометрический расходомер.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: "Что-то тут концом пахнет". 8516 — 
| 8103 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Цилиндр радиуса R и массы т скатывается по наклонной плоскости, образующей угол а с горизонтом (рис. 6.10). Центр масс С лежит на оси цилиндра, а его момент инерции относительно этой оси равен /. Цилиндр совершает плоское движение. Первым делом следует определить функции, при помощи которых можно описать это движение. В данной задаче ось х удобно направить вдоль прямой, являющейся траекторией движения центра масс. При этом движение цилиндра можно описать посредством двух функций, выражающих зависимости от времени t координаты х центра масс и угла
Из этой формулы видно, что сумма моментов сил тяжести такова, как будто все эти силы приложены к центру масс тела.
Моменты сил тд и N относительно оси z’, проходящей через центр масс, равны нулю, так как линии действия этих сил проходят через ось z 1 . При этом уравнение (6.23) принимает вид
1. Предположим, что цилиндр катится с проскальзыванием. В этом случае справедлив закон Амонтона
где знак плюс или минус следует оставить в зависимости от того, как направлен вектор силы трения. При этом уравнения (6.42) — (6.45) образуют систему с четырьмя неизвестными: х = x(t),
Преподаватель сказал, что нужно решать через:
Iε= →
I* R= *Тут надо расписать *
И далее уже вывести ускорение
PS "I"-момент инерции; — a-тау, вроде как, тангенциальное ускорение
Загрузка...
