С тем, чтобы проиллюстрировать применение законов динамики твёрдого тела, решим задачу о скатывании цилиндра с наклонной плоскости (рис. 10.5).
Сплошной цилиндр массы m и радиуса R скатывается без проскальзывания с наклонной плоскости. Угол наклона плоскости — a, а высота Н (Н » R). Начальная скорость цилиндра равна нулю. Определим время скатывания — Т и скорость центра масс цилиндра у основания наклонной плоскости.
При качении цилиндра на него действуют три силы: сила тяжести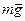 
, упругая сила реакции опоры 
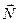и сила трения покоя 
(ведь качение без проскальзывания!).
Представим это движение суммой двух движений: поступательного со скоростью VC, с которой движется ось цилиндра, и вращательного вокруг оси цилиндра с угловой скоростью w.
. (10.9)
Эта связь скоростей поступательного и вращательного движений следует из условия «движение без проскальзывания».
Продифференцировав уравнение (10.9) по времени, получим соотношение углового и линейного ускорений цилиндра:
, то есть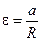 
.
Воспользовавшись теоремой о движении точки центра масс, опишем поступательное движение цилиндра:
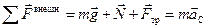. (10.10)
Для описания вращения воспользуемся основным уравнением динамики вращательного движения:
Спроецировав уравнение (10.10) на направления осей x и y, получим два скалярных уравнения:
Обратимся теперь к уравнению (10.11). Из трёх названных сил момент относительно оси цилиндра создаёт только сила трения:
.
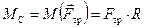Момент инерции сплошного цилиндра относительно его оси равен (см. лекцию №9):
.
Учитывая всё это, уравнение (10.11) перепишем так:
. (10.14)
Решая совместно уравнения (10.12) и (10.14), получим следующие значения неизвестных величин:
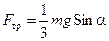; (10.15)
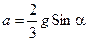. (10.16)
Из уравнения (10.15) следует, что с увеличением угла наклона a должна возрастать и сила трения покоя Fтр. Но, как известно, её рост ограничен предельным значением:
. (10.17)
Так как сила трения покоя (10.15) не может превышать предельного значения (10.17), то должно выполняться неравенство:
Отсюда следует, что скатывание будет происходить без проскальзывания до тех пор, пока угол a не превзойдёт значения aпред:
Здесь m — коэффициент трения цилиндра по плоскости.
Линейное ускорение цилиндра (10.16) величина неизменная, следовательно, поступательное движение цилиндра равноускоренное. При таком движении без начальной скорости цилиндр достигнет основания наклонной плоскости за время:
.
Здесь: l = 
— длина плоскости;
a =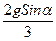
, (см.10.16).
Значит, время скатывания:
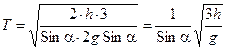. (10.18)
Вычислим конечную скорость поступательного движения оси цилиндра:
. (10.19)
Заметим, что эту задачу можно решить проще, воспользовавшись законом сохранения механической энергии.
В системе, правда, присутствует сила трения, но её работа равна нулю, поскольку точка приложения этой силы в процессе спуска остаётся неподвижной: ведь движение происходит без проскальзывания. Раз нет работы силы трения, механическая энергия системы не меняется.
Рассмотрим энергию цилиндра в начальный момент — на высоте h и в конце спуска. Полная энергия цилиндра в этих положениях одинакова:
.
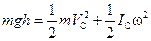Вспомним, что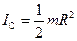 
и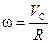 
. Тогда уравнение закона сохранения энергии можно переписать так:
.
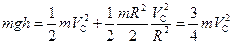Отсюда легко найдём конечную скорость цилиндра:
,
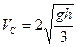которая блестяще подтверждает полученный нами ранее результат (10.19).
Лекция 11 «Элементы механики жидкости»
1. Давление жидкости. Законы гидростатики.
2. Стационарное течение жидкости. Уравнение неразрывности потока.
3. Основной закон динамики для идеальной жидкости. Уравнение Бернулли.
4. Применение уравнения Бернулли для решения задач гидродинамики.
4.1. Истечение жидкости из сосуда.
4.2. Манометрический расходомер.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8547 — 
| 7401 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
ЦЕЛЬ: приобрести навык расчёта момента инерции тел, состоящих из простых элементов, определить момент инерции тела относительно мгновенной оси вращения расчётным и экспериментальным методом
ОБОРУДОВАНИЕ: установка, набор тел, секундомер
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В работе используются тела, осью которых является цилиндрический стержень радиусом r. Одно из рис. 1) помещают на параллельные направляющие 2, образующие с горизонтом углы α1 и α2.
Если тело отпустить, то оно, скатываясь, достигнет нижней точки и, двигаясь далее по инерции, поднимется вверх по направляющим. Движение тела, при котором траектории всех точек лежат в параллельных плоскостях, называется плоским. Плоское движение можно представить двумя способами: либо как совокупность поступательного движения тела со скоростью центра масс и вращательного вокруг оси, проходящей через центр масс; либо как только вращательное движение вокруг мгновенной оси вращения (MOB), положение которой непрерывно изменяется. В нашем случае эта мгновенная ось Z проходит через точки касания направляющих с движущимся стержнем.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ
При скатывании тело, опускаясь с высоты 
проходит путь l0, а поднимаясь по инерции на высоту 
проходит путь l. В нижней точке скорость поступательного движения центра масс 
, а угловая скорость тела
, (1)
где t — время движения от верхней точки до нижней, г — радиус стержня (оси).
На скатывающееся тело действует момент сил сопротивления Мтр. Работа его на пути l0 равна A = Мтрφ где угловой путь φ = l0/r.
Закон сохранения энергии на отрезке пути l0 имеет вид
, (2)
где J — момент инерции скатывающегося тела относительно MOB, m — масса тела, включающая в себя массу стержня.
При движении тела вниз с высоты h0 и вкатывании его на высоту h работа сил сопротивления на пути (l + l0) равна убыли потенциальной энергии
. (3)
Запишем формулу для определения момента инерции динамическим методом:
(4)
Здесь величина (α1 и α2) является константой для данной установки.
Момент инерции тела относительно MOB определяется теоремой Штейнера J = J0 + ma2, (5)
где J0 — момент инерции, относительно центра масс; а — расстояние от центра масс тела до оси вращения (в этом опыте a = r).
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание 1. Расчёт момента инерции тела сложной формы
Для расчёта момента инерции маховика I необходимо измерить массу тела (написана на телах) или объём (массу рассчитать, используя плотность) и радиусы цилиндрических тел.
1. Исследуйте форму тела. Приняв во внимание, что момент инерции любого тела равен сумме моментов инерции отдельных его элементов, мысленно разделите исследуемое тело на простые элементы, для которых формулы расчёта величины Ji даны в табл. 1.
2. Сделайте эскиз исследуемого тела, а если необходимо, то и его элементов, обозначая символами все размеры, подлежащие измерению. Например, тело (рис. 1а) состоит из насаженных на вал 1 шкива 2 и маховика 3 с двумя отверстиями 4. Это тело можно представить (рис. 16) как совокупность трёх сплошных цилиндров 1, 2 и 3 за вычетом двух малых дисков расположенных на месте отверстий маховика.
Для расчёта момента инерции такого тела необходимо знать массы указанных элементов, их радиусы, а также расстояние а от центра отверстий до оси вращения.
(5)
В случае, если массы тi неизвестны, то для их определения через плотность и объём деталей нужно измерить ещё их длины l1, l2 и l3.
Лабораторная работа №1:
«Изучение движения тела под действием постоянной силы
1) доказать, что движение тела — равноускоренное;
2) вычислить ускорение движения.
Оборудование: штатив, направляющая рейка, каретка, секундомер с двумя датчиками.
На тело действуют 3 силы. Если геометрическая сумма сил больше нуля, тело движется с ускорением.
Согласно второму закону Ньютона 
Установить направляющую рейку при помощи штатива под углом 30 0 ( h =22 см).
К секундомеру подключить датчики. Один датчик установить на расстоянии 6 см от начала рейки. Второй- датчик будет устанавливаться на расстоянии 25см, 30см, 35см.
Каретку устанавливаем на направляющую рейку так, чтобы магнит располагался на расстоянии менее 1 см от первого датчика.
Отпустить каретку и определить время движения каретки между датчиками. Опыт повторить 3 раза. Результаты измерений записать в таблицу.
, м / с 2
1. При движении с ускорением, (если v =0 ) 
Должно выполняться соотношение 
Проверьте выполнение этого равенства. Сделайте вывод.
2. По результатам опытов вычислите ускорение:
;
Результаты занесите в таблицу.
3. Вычислите максимальную относительную погрешность:
4.Вычислите абсолютную погрешность: 
Цель работы:
1) доказать, что движение тела — равноускоренное;
2) вычислить ускорение движения.
Оборудование: штатив, направляющая рейка, каретка, секундомер с двумя датчиками.
На тело действуют 3 силы. Если геометрическая сумма сил больше нуля, тело движется с ускорением.
Согласно второму закону Ньютона
- Гайсинюк Марина НиколаевнаНаписать 10775 27.05.2018
Номер материала: ДБ-1644208
-
27.05.2018 422
-
27.05.2018 112
-
27.05.2018 199
-
27.05.2018 501
-
27.05.2018 601
-
27.05.2018 262
-
27.05.2018 84
-
27.05.2018 69
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Загрузка...
