Теорема сложения вероятностей несовместных событий.Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Теорема сложения вероятностей совместных событий.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Для трех совместных событий имеет место формула
Событие, противоположное событию А (т.е. не наступление события А), обозначают 
. Сумма вероятностей двух противоположных событий равна единице:
Вероятность наступления события А, вычисленная в предположении, что событие В уже произошло, называется условной вероятностью события А при условии В и обозначается 
или 
.
Если А и В 
независимые события, то
Событие А,В,С,… называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением других событий по отдельности или в любой их комбинации.
Теорема умножения вероятностей
Теорема умножения вероятностей независимых событий.Вероятность совместного появления двух независимых событий равна произведению вероятностей
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле
Теорема умножения вероятностей зависимых событий.Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
Формула полной вероятности. Формула Байеса
Пусть событие (гипотезы) 
образуют полную группу событий и при наступлении каждого из них, например 
, событие А может наступить с некоторой условной вероятностью 
Тогда вероятность наступления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
где 
Формула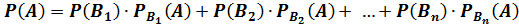 
называется формулой полной вероятности.
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) , которые образуют полную группу событий. Если событие А уже произошло, то вероятность гипотез могут быть переоценены по формуле Байеса(формуле вероятности гипотез):
,
где 
вероятность каждой из гипотез после испытания, в результате которого наступило событие, А; 
условная вероятность события А после наступления события 
а 
находится по формуле полной вероятности
Повторение испытаний. Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимы относительно события А.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А равна p(где 0 
событие А наступит ровно k раз (безразлично, какой последовательности), находится по формуле Бернулли:
где 
Тема 5.1 Основы теории вероятностей
Исследовательская работа. Решение задач
Упражнения
1.Найдите число размещений: 
2.Вычислите: 
3. 30 учащихся обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек?
4.Сколькими способами из восьми кандидатов можно выбрать три лица на три должности?
5.Решите уравнения: 
6. Сколькими способами можно составить список из 10 человек?
7.Сколькими способами можно распределить 12 классных комнат под 12 учебных кабинетов?
8. В ящике с деталями оказалось 300 деталей I сорта, 200 деталей II сорта и 50 деталей III сорта. Наудачу вынимают одну из деталей. Чему равна вероятность вынуть деталь I, II или III сорта?
9.В урне находится 20 белых и 15 черных шаров. Наудачу вынимают один шар, который оказался белым, и откладывают его в сторону. После этого берут еще один шар. Найдите вероятность того, что это шар также окажется белым.
10.В ящике в случайном порядке положены 10 деталей, из которых 4 стандартных. Контролер взял наудачу 3 детали. Найдите вероятность того, что хотя бы одна из взятых деталей оказалась стандартной.
11.В урне находится 10 белых, 15 черных, 20 синих и 25 красных шаров. Найдите вероятность того, что вынутый шар окажется: 1) белым; 2) черным или красным.
12.Рабочий обслуживает два автомата, работающих независимо друг от друга. Вероятность того, что в течении часа первый автомат не потребует внимание рабочего, равна 0,8, а для второго автомата эта вероятность равна 0,7. Найдите вероятность того, что в течение часа ни один из автоматов не потребует внимание рабочего.
13.В урне находится 6 шаров, из которых 3 белых. Наудачу вынут один за другим два шара. Вычислите вероятность того, что оба шара окажутся белыми.
14.В урну, содержащую три шара, положили белый шар, после чего из нее наугад вынули один шар. Найдите вероятность того, что извлеченный шар окажется белым, если все возможные предположения о первоначальном составе шаров (по цвету) равновозможные.
15.В ящике сложены детали: 16 деталей с первого участка, 24-со второго и 20-с третьего. Вероятность того, что деталь, изготовленная на втором участке, отличного качества, равна 0,6, а для деталей, изготовленных на первом и третьем участках, вероятности равна 0,8. Найдите вероятность того, что наудачу извлеченная деталь окажется отличного качества.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Ответы на вопрос
в сплаве олова и железа олова содеожется 65%. масса сплава 800г. сколько в сплаве железа( в
800*65100=520 г олова
800-520=280 г железа
опыт: выбор 2-х карточек из 4-х. всего исходов опыта — число сочетаний из 4 по 2, то есть 6. перечислим все исходы — пары чисел на карточках.
видно, что событию: сумма нечетна
благоприятствуют 4 исхода
класситческое определение вероятности. вероятность события получаем делением 4 на 6. ответ: 2/3.
Одно из важнейших правил комбинаторики – правило произведения.
Правило произведения. Если объект A1 может быть выбран k1 способами, затем для каждого из таких выборов объекта A1 другой объект A2 может быть выбран k2 способами, затем для каждого из таких выборов и объекта A1, и объекта A2 третий объект A3 может быть выбран k3 способами и т.д., наконец, объект Am может быть выбран km способами, тогда объект «A1 и A2, и A3, и …, и Am» может быть выбран 
способами.
Сочетаниями из n различных элементов по m элементов (m≤n)называют комбинации из m элементов, которые составлены из данных n элементов и отличаются хотя бы одним элементом. Число сочетаний из n элементов по m обозначают 
или 
и вычисляют по формуле: 
, где n! (читают «эн факториал») – произведение натуральных чисел от 1 до n: 
, причем 0!=1.
Пример 1. Сколькими способами между тремя сотрудниками можно распределить две различные путевки?
Решение. Претендент на первую путевку – один из трех сотрудников – может быть выбран тремя способами. Если первая путевка досталась первому сотруднику, то вторая может достаться или второму, или третьему сотруднику. Если первая путевка досталась второму сотруднику, то вторая может достаться или первому, или третьему сотруднику. Если первая путевка досталась третьему сотруднику, то вторая может достаться или первому, или второму сотруднику. Таким образом, для каждого способа распределения первой путевки претендент на вторую путевку может быть выбран двумя способами. Две различные путевки (и первая, и вторая) по правилу произведения могут быть распределены шестью способами:
1) первому и второму сотрудникам;
2) первому и третьему сотрудникам;
3) второму и первому сотрудникам;
4) второму и третьему сотрудникам;
5) третьему и первому сотрудникам;
6) третьему и второму сотрудникам.
Ответ: шестью способами.
Пример 2. Сколькими способами между тремя сотрудниками можно распределить две одинаковые путевки?
Решение. Искомое число равно числу способов выбора из трех сотрудников двух претендентов на путевки. Поскольку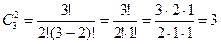 
, то распределить две одинаковые путевки между тремя сотрудниками можно тремя способами.
Ответ: тремя способами.
7.1.1. Сколькими способами можно составить флаг, содержащий три горизонтальные полосы различных цветов, если имеется материал пяти цветов? Ответ: 60.
7.1.2. Сколькими способами из группы студентов в двадцать пять человек можно выбрать старосту и физорга? Ответ: 600.
7.1.3. Десять спортсменов разыгрывают одну золотую, одну серебряную и одну бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами? Ответ: 720.
7.1.4. Студентам нужно сдать четыре экзамена за восемь дней. Сколькими способами можно составить расписание сдачи экзаменов? Ответ: 1680.
7.1.5. Сколько словарей нужно издать, чтобы непосредственно выполнить переводы с любого из трех языков: русского, английского, французского — на любой другой из этих трех языков? Ответ: 6.
7.1.6. Сколькими способами можно рассадить на скамейке трех человек? Ответ: 6.
7.1.7. Сколькими способами пять книг разных авторов можно расставить на полке? Ответ: 120.
7.1.8. В конкурсе по пяти номинациям участвуют десять кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены различные призы? одинаковые призы? Ответ: 30240; 252.
7.1.9. В хоккейном турнире участвуют шесть команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире? Ответ: 15.
7.1.10. Сколькими способами читатель может выбрать три книжки из пяти имеющихся различных книг? Ответ: 10.
7.1.11. Сколькими способами можно в строчку написать три плюса и два минуса? Ответ: 10.
7.1.12. В лабораторной клетке содержат пять белых и пять коричневых мышей. Найдите число способов выбора: а) трех мышей, если они могут быть любого цвета; б) трех белых мышей. Ответ: 120; 10.
7.1.13. В ящике двадцать кубиков, среди которых пятнадцать окрашены. Сколькими способами можно взять пять кубиков? пять окрашенных кубиков? Ответ: 15504; 3003.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8547 — 
| 7401 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Загрузка...
