Сколько оборотов сделает до полной остановки маховик

Задача

Маховое колесо вращается равномерно с угловой скоростью 16 с -1 . Определить, сколько оборотов сделает колесо за 5 мин вращения.

Решение

1) Находим угол поворота маховика в радианах (t = 5 мин =300 с):

Находим число оборотов маховика:

2) Возможно другое решение. Переведем угловую скорость в об/мин:

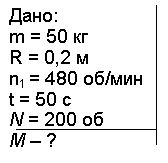
Задача 1. Маховик в виде диска массой m = 50 кг и радиусом R = 0,2 м был раскручен до частоты вращения n₁ = 480 об/мин и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, если:

1) маховик остановился через t = 50 с;

2) маховик до полной остановки сделал N = 200 оборотов.

Решение. 1) По основному закону динамики вращательного движения тела , (7.6)т.е. изменение момента импульса вращающегося тела равно произведению момента силы трения на время действия этого момента, где J – момент инерции маховика; w1 и w2 – начальная и конечная скорости маховика.

Так как w₂ = 0, Dt = t, то , где , тогда

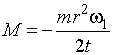. (7.7)

Выразим угловую скорость через частоту w₁ = 2pn₁ и подставим в (7.7), получим:

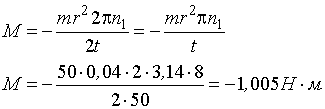
1) Работа силы трения равна изменению кинетической энергии диска:

, (7.8)

а так как w₂ = 0, то

. (7.9)

С другой стороны,

, (7.10)

где 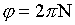. Приравниваем выражения (7.9) и (7.10), получаем:

Знак «-» означает, что момент сил трения оказывает тормозящее действие.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9516 — | 7342 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

2017-05-21
Маховик, массу которого $m = 5 кг$ можно считать распределенной по ободу радиуса $r = 20 см$, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой $n = 720 мин^<-1>$ (рис.). При торможении маховик останавливается через промежуток времени $Delta t = 20 с$. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

Если тормозящий момент постоянен, то движение маховика равнозамедленное и основное уравнение динамики вращательного движения можно записать в виде

$J Delta vec < omega>= vec Delta t$, (1)

где $Delta vec < omega>= vec< omega>_ — vec< omega>_<0>$ — изменение угловой скорости за интервал $Delta t, vec$ — искомый тормозящий момент.

Число оборотов $N$ может быть найдено как кинематически, так и по изменению кинетической энергии, равному работе, совершенной тормозящей силой.

Векторному уравнению (1) соответствует скалярное уравнение

$J Delta omega = M Delta t$, (2)

где $Delta omega$ и $M$ — модули соответствующих векторов. Из условия задачи следует, что

$Delta omega = | omega_ — omega_ <0>| = omega_ <0>= 2 pi n, J = mr^<2>$. (3)

Последняя из формул (3) справедлива, поскольку масса маховика распределена по ободу.

Подставив выражения (3) в (2), получим $mr^ <2>cdot 2 pi n = M Delta t$, откуда

$M = 2 pi n mr^ <2>/ Delta t = 0,75 Н cdot м$.

Очевидно, что векторы $vec$ и $Delta vec< omega>$ направлены в сторону, противоположную вектору $vec< omega>_<0>$.

Угловое перемещение, пройденное маховиком до остановки,

$Delta phi = omega_ <0>Delta t — epsilon ( Delta t)^<2>/2ш$. (4)

Учитывая, что $omega_ = omega_ <0>- epsilon Delta t = 0$, преобразуем выражение (4):

$Delta phi = omega_ <0>Delta t/2$.

Заменив $Delta phi$ и $omega_<0>$ соответственно на $2 pi N$ и $2 pi n$, где $N$ — искомое число оборотов, которое маховик сделает до полной остановки, окончательно получим