Булевы функции 1 названы в честь английского математика ХIХ века Дж. Буля, который впервые применил алгебраические методы для решения логических задач. Они образуют самый простой нетривиальный класс дискретных функций — их аргументы и значения могут принимать всего два значения (если мощность множества значений функции равна 1, то это тривиальная функция — константа !). С другой стороны, этот класс достаточно богат и его функции имеют много интересных свойств. Булевы функции находят применение в логике, электротехнике, многих разделах информатики.
Обозначим через B двухэлементное множество <0,1>. Тогда
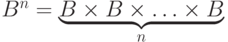
это множество всех двоичных последовательностей (наборов, векторов) длины n. Булевой функцией от n переменных (аргументов) называется любая функция f(x1, xn): B n -> B . Каждый из ее аргументов xi, 1 k . В нашем случае B=<0, 1>, а A = B n . Тогда m=2 и k= |B n | = 2 n . Отсюда следует утверждение теоремы.
Имеется несколько различных способов представления и интерпретации булевых функций. В этом разделе мы рассмотрим геометрическое и табличное представления, а также представление с помощью логических формул. В "Эквивалентность формул и нормальные формы" будет показано, как булевы функции можно представлять с помощью формул специального вида — дизъюнктивных и конъюнктивных нормальных форм и многочленов Жегалкина. Кроме того, в лекциях "Предварительные сведения" и "Индукция и комбинаторика" (курс "Введение в схемы, автоматы и алгоритмы") будет рассмотрено еще два способа представления булевых функций: логические схемы и упорядоченные бинарные диаграммы решений.
Геометрическое представление
Bn можно рассматривать как единичный n-мерный куб. Каждый набор из нулей и единиц длины n задает вершину этого куба. На рис. 3.1 представлены единичные кубы Bn при n=3,4.
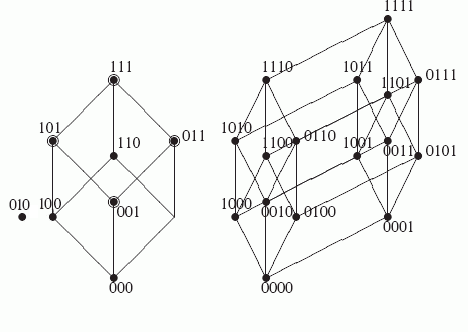
Рис. 3.1.
При этом существует естественное взаимно однозначное соответствие между подмножествами вершин n-мерных единичных кубов и булевыми функциями от n переменных: подмножеству 
соответствует его характеристическая функция
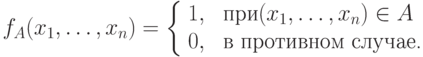
Например, верхней грани куба B 3 (ее вершины выделены на рисунке) соответствует функция f: f(0,0,1)=f(0,1,1)=f(1,0,1)=f(1,1,1) =1 и f(0,0,0)=f(0,1,0)=f(1,0,0)=f(1,1,0) =0. Очевидно, что указанное соответствие действительно взаимнооднозначное: каждая булевая функция f от n переменных задает подмножество Af=<(x1, . xn)|f(x1, . xn)=1> вершин B n . Например, функция, тождественно равная 0, задает пустое множество 
, а функция, тождественно равная 1, задает множество всех вершин B n .
Табличное представление
Булевы функции от небольшого числа аргументов удобно представлять с помощью таблиц. Таблица для функции f(x1, . xn)имеет n+1 столбец. В первых n столбцах указываются значения аргументов x1, . xn , а в (n+1) -ом столбце значение функции на этих аргументах — f(x1, . xn) .
| Таблица 3.1. Табличное представление функции f(x1, . xn) | ||||||
| x1 | . | . | . | xn-1 | xn | f(x1, . xn) |
| . | . | . | f(0, . 0,0) | |||
| . | . | . | f(0, . 0,1) | |||
| . | . | . | f(0, . 1,0) | |||
| . | . | . | . | . | . |  |
| . | . | . | f(1, . 1,1) |
Наборы аргументов в строках обычно располагаются в лексикографическом порядке:
существует такое 
, что при 
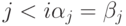, а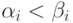 
.
Если эти наборы рассматривать как записи чисел в двоичной системе счисления, то 1-ая строка представляет число 0, 2-ая — 1, 3-я — 2,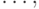 
а последняя — 2 n -1 .
При больших n табличное представление становится громоздким, например, для функции от 10 переменных потребуется таблицас 1024 строками. Но для малых n оно достаточно наглядно.
Формулы
Как мы видели, геометрическое и табличное представления булевых функций подходят лишь для функций с небольшим числом аргументов. Формулы позволяют удобно представлять многие функции от большего числа аргументов и оперировать различными представлениями одной и той же функции.
Пусть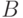 
— некоторое (конечное или бесконечное) множество булевых функций. Зафиксируем некоторое счетное множество переменных V=1, X2, . > . Определим по индукции множество формул над 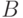с переменными из V. Одновременно будем определять числовую характеристику 
формулы 
называемую ее глубиной, и множество ее подформул.
Определение 3.2.
1. Базис индукции. Каждая переменная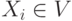 
и каждая константа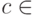 
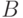является формулой глубины 0, т.е. dep(Xi)=dep(c)=0 . Множество ее подформул состоит из нее самой.
2. Шаг индукции. Пусть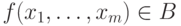 
и A1, . , Am — формулы, и max <dep(Ai) | i = 1. m> = k . Тогда выражение 
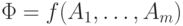является формулой, ее глубина равна k+1, а множество подформул 
включает саму формулу и все подформулы формул A1, . Am.
Каждой формуле 
сопоставим булеву функцию, которую эта формула задает, используя индукцию по глубине формулы.
Базис индукции. Пусть 
. Тогда 
или 
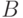. В первом случае задает функцию 
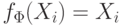, во втором — функцию, тождественно равную константе c.
Шаг индукции. Пусть — произвольная формула глубины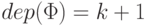 
. Тогда 
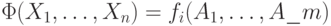, где 
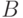и A1, . Am — формулы, для которых max1
Сколько существует монотонных булевых функций от 3 переменных?
задан 14 Янв ’18 17:14
1 ответ
В отличие от других предполных классов, для количества монотонных функций от n переменных, хорошей общей формулы не имеется. Поэтому считать придётся вручную. Способов можно предложить несколько. Один из них такой: сразу учтём 2 константы. Остальные монотонные функции представляются в виде дизъюнкции элементарных конъюнкций. При этом более "слабые" члены не учитываются, что гарантирует единственность. Это означает, что если одна конъюнкция "содержит" другую — в том смысле, как xz "содержит" и x, и z, то x V xz равно x. Поэтому наличие члена xz исключает наличие более "слабых" членов x и z.
Тогда, если есть xyz, то больше ничего нет. Предположим, что члена 3-й степени нет, а члены 2-й степени есть. Если их три, то получается функция голосования xy V xz V yz. Других членов нет. Если их два, то это функция xy V xz, или симметричная ей. Всего таких 3 штуки. Других членов снова нет. Если есть только один член — скажем, xy, то он идёт или сам по себе, или вместе с z, то есть функция равна xy V z. С учётом симметрии, это ещё 6 случаев. Наконец, если члены имеют только первую степень, то функций будет 2^3-1=7 по числу непустых подмножеств в .
Теперь аккуратно всё складываем: 2+1+1+3+6+7=20. Это ответ.
Вот ещё один способ. От двух переменных имеется ровно 6 монотонных функций: две константы, две переменные, конъюнкция и дизъюнкция. Это легко проверяется. В виде векторов их легко выписать (в лексикографическом порядке): 0000, 0001, 0011, 0101, 0111, 1111. Теперь заметим, что при фиксации значения одной переменной у монотонной функции, это свойство сохраняется. Если для функции f(x,y,z) мы фиксируем x=0, то получим один из этих 6 наборов. Если фиксируем x=1, то снова получается набор из списка, который покоординатно не меньше предыдущего. Поэтому остаётся для каждого набора списка подсчитать число покоординатно не меньших, и всё сложить. Это даёт 6+5+3+3+2+1=20. Ответ тот же.
Дата добавления: 2015-07-23 ; просмотров: 4667 ; Нарушение авторских прав
Булевы функции 1) названы в честь английского математика ХIХ века Дж. Буля, который впервые применил алгебраические методы для решения логических задач. Они образуют самый простой нетривиальный класс дискретных функций — их аргументы и значения могут принимать всего два значения (если мощность множества значений функции равна 1, то это тривиальная функция — константа !). С другой стороны, этот класс достаточно богат и его функции имеют много интересных свойств. Булевы функции находят применение в логике, электротехнике, многих разделах информатики.
Обозначим через B двухэлементное множество <0,1>. Тогда
это множество всех двоичных последовательностей (наборов, векторов) длины n. Булевой функцией от n переменных (аргументов) называется любая функция f(x1, xn): B n -> B . Каждый из ее аргументов xi, 1 k . В нашем случае B=<0, 1>, а A = B n . Тогда m=2 и k= |B n | = 2 n . Отсюда следует утверждение теоремы.
Суперпозицией булевых функций f0 и f1. fn называется функция f(x1. xm) = f0(g1(x1. xm). gk(x1. xm)), где каждая из функций gi(x1,. xm) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f1. fn.
19. Число булевых функций от n аргументов. Выражение булевых функций через конъюнкцию, дизъюнкцию и отрицание (теорема о разложении функции по переменной и теорема о представлении булевых функций через конъюнкцию, дизъюнкцию и отрицание).
Дизъюнктивная нормальная форма
Простой конъюнкцией или конъюнктом называется конъюнкция некоторого конечного набора переменных или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций. Элементарная конъюнкция
§ правильная, если в неё каждая переменная входит не более одного раза (включая отрицание);
§ полная, если в неё каждая переменная (или её отрицание) входит ровно 1 раз;
§ монотонная, если она не содержит отрицаний переменных.
Например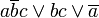 
— является ДНФ.
Совершенной дизъюнктивной нормальной формой или СДНФ относительно некоторого заданного конечного набора переменных называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Например: 
.
Легко убедиться, что каждой булевой функции соответствует некоторая ДНФ, а функции отличной от тождественного нуля — даже СДНФ. Для этого достаточно в таблице истинности этой функции найти все булевы векторы, на которых её значение равно 1, и для каждого такого вектора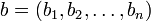 
построить конъюнкцию 
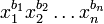, где 
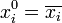. Дизъюнкция этих конъюнкций является СДНФ исходной функции, поскольку на всех булевых векторах её значения совпадают со значениями исходной функции. Например, для импликации 
результатом является 
, что можно упростить до 
.
Конъюнктивная нормальная форма
Конъюнктивная нормальная форма1 (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.
Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».
КНФ может быть преобразована к эквивалентной ей ДНФ путём раскрытия скобок по правилу:
которое выражает дистрибутивность конъюнкции относительно дизъюнкции. После этого необходимо в каждой конъюнкции удалить повторяющиеся переменные или их отрицания, а также выбросить из дизъюнкции все конъюнкции, в которых встречается переменная вместе со своим отрицанием. При этом результатом не обязательно будет СДНФ, даже если исходная КНФ была СКНФ. Точно также можно всегда перейти от ДНФ к КНФ. Для этого следует использовать правило
выражающее дистрибутивность дизъюнкции относительно конъюнкции. Результат нужно преобразовать описанным выше способом, заменив слово «конъюнкция» на «дизъюнкция» и наоборот.
Загрузка...
