Сколько воскресений в месяце

Что ты хочешь узнать?

Ответ

Проверено экспертом

В одной неделе есть одно воскресенье. То есть из семи последовательных дней один будет воскресеньем.

Для 4-х в месяце воскресеньев нужно 7*4 = 28 дня максимум, 22 дня минимум (если отсчет идет с воскресенья)

Максимум: 35(начиная с понедельника)

Минимум: 29 (начиная с воскресенья)

• Комментарии
• Отметить нарушение

Ответ

Проверено экспертом

1 месяц — 28 дней, 29 дней, 30 дней, 31 день

1 неделя — это 7 дней

28 : 7 = 4 недели — то есть, если в месяце 28 дней, то 4 воскресенья.

29 : 7 = 4 недели ( 1 день остаток) — если в месяце 29 дней и месяц начинается с воскресенья , то может быть 5 воскресений.

30 : 7 = 4 недели ( 2 дня остатка) — тоже может быть 5 воскресений.

31 : 7 = 4 недели ( 3 дня остатка) — тоже может быть 5 воскресений.

если месяц содержит больше 4 недель, хотя бы на 1 день, то может быть 5 воскресений. ( месяц будет начинаться с воскресенья)

Ответы на вопрос

при делении вторая дробь(1/7) переворачивается и делается умножение:

ответ: 16 яиц купила мама; 6 яиц осталось до обеда.

пошаговое объяснение: решаем с конца:

(2+1)÷(1/2)=6 (яиц) осталось до обеда.

(6+2)÷(1/2)=16 (яиц) всего купила мама.

в числителе: 2 в степени n, а в знаменателе: n в степени 4

1. Может ли быть в одном месяце быть 5 понедельников и 5 четвергов? Обоснуйте ответ.

Если в месяце 31 день, и он начинается с понедельника, то в нём может быть 5 понедельников, 5 вторников и 5 сред, но остальных дней недели по четыре, так как 5+5+5+4+4+4+4=31. Ответ: не может.

2. Может ли в феврале высокосного года быть 5 понедельников и 5 вторников? Ответ обоснуйте.

Только в феврале высокосного года может быть 5 понедельников и по 4 остальных дней недели, т.е. в сумме – 29 дней. Ответ: не может.

3. В феврале 2004 года 5 воскресений, а всего – 29 дней. На какой день недели приходится 23 февраля 2004 года?

Если в феврале 29 дней и 5 воскресений, то первое воскресение будет 1 февраля. Отсюда 23 февраля – понедельник.

4. В некотором месяце три пятницы пришлись на чётные числа. Какой день недели был 15 числа этого месяца?

Три пятницы, выпадающие на чётные числа месяца, могут быть только 2, 16 и 30 числа. 15 числа был четверг.

5. Известно. Что 1 декабря приходится на среду. На какой день недели приходится 1 января следующего года?

Среда 1, 8, 15, 22, и 29 декабря, четверг 30, пятница 31. Ответ: суббота 1 января следующего года.

6. В некотором месяце три воскресенья пришлись на чётные числа. Какой день недели был 20 числа этого месяца?

Четные воскресенья 2, 16, 28. Значит 20 число этого месяца – четверг.

7. Какое наибольшее число воскресений может быть в году?

8. Какое самое большое число месяцев с пятью воскресениями может быть в году?

5 месяцев. Обычный год при этом должен начинаться с воскресенья, а високосный – с субботы или воскресенья.

9. В каком-то году некоторое число ни в одном месяце не было воскресеньем. Какое это могло быть число?

31-е число и только одно. Например, в 2007 году ни одно воскресенье не было 31 числом.

10. В некотором месяце три субботы пришлись на четные числа. Какой день недели был 28-го числа этого месяца?

Пусть первая «четная» суббота пришлась на число, которое обозначим через х ( х – четное число). Следующая четная суббота будет через две недели, т.е. (х+14) –го числа, а третья «четная» суббота – (х+28) –го числа. Но в месяце не более 31 дня, следовательно, х+28≤ 31. У этого неравенства одно еётное решение х=2. Тогда третья «четная» суббота была 30-го числа, а 28-го был четверг.

11. В некотором месяце три пятницы пришлись на четные числа. Какой день недели был 15 числа этого месяца?

12. В некотором месяце три воскресенья пришлись на четные числа. Какой день недели был 20 числа этого месяца?

13. Докажите, что первый и последний день 2010 года – это один и тот же день недели.

2010 год не високосный 2. Обычный год содержит 365=52х7+1 дней, т.е. 52 полных недели плюс один день. Поэтому любой обычный год начинается и заканчивается на один и тот же день недели. Для 2010 года это будет пятница.

14. В некотором месяце понедельников больше, чем вторников, а воскресений больше, чем суббот. Какой день недели был 5-го числа этого месяца? Мог ли этот месяц быть декабрем?

За 4 недели, с 1 по 28-е число, каждый день недели встречается ровно 4 раза, поэтому из условия следует, что 29-е – воскресенье, 30-е – понедельник, а 31-го числа в этом месяце нет. Следовательно, месяц, о котором идет речь, начался с воскресенья, а его 5-е число было четвергом. Данный месяц декабрём быть не мог: в декабре 31 день.

15. В некотором году три месяца подряд содержали всего по четыре воскресенья. Докажите, что один из этих месяцев – февраль.

Если февраль не входит в указанные «три месяца подряд», то сумма дней – 91 или 92. Но 91=7х13, 92=7х13+1, т. е в этом случае три месяца содержат 13 полных недель, значит, и каждый день недели, в том числе воскресенье, содержится 13 раз, и условие не выполняется. Тем самым доказано, что один из трех месяцев должен быть февралём, причем в обычном году достаточно, чтобы из трёх месяцев был февралём, а в високосном – эти три месяца: февраль(29), март(31), апрель(30). К тому же необходимо, чтобы последний день третьего месяца был субботой.

16. У большинства Петиных одноклассников день рождения в 1995 году пришёлся на четверг. В 1996 году у большинства одноклассников он пришёлся на пятницу. А на какой день недели он приходился в 1997 году?

1995 и 1997 годы не високосные (по 365 дней), а 1996 – високосный (366 дней). При переходе от 1995 года к 1996 году любое число сместится на один день недели вперёд. Но при переходе от 1996-го високосного, смещение будет на два дня вперёд, т. е. день рождения, приходившийся на пятницу, сместится на воскресенье.

17. Год 2000 обозначается всего двумя римскими цифрами ММ. Какой год из прошедших 2000 лет содержит максимальное количество римских цифр в своей записи?

18. Один человек обнаружил в 1937 году, что в 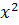-м году ему было х лет, и сказал: «Если к числу моих лет прибавить порядковый номер месяца моего рождения, то получится квадрат дня моего рождения. Когда родился этот человек?

Если человек жил в 1937 году, то в 1849 году ему не могло быть 43 года: 1849=43 2 . Следующая возможность – ему было 44 года в 1936 году: 1936=44 2 . В силу заданных условий, 44+m=d 2 ; 0

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8547 — | 7401 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно