Содержание
Ра́диус-ве́ктор (обычно обозначается r → <displaystyle <vec 

Для произвольной точки в пространстве радиус-вектор — это вектор, идущий из начала координат в эту точку.
Длина, или модуль радиус-вектора — расстояние, на котором точка находится от начала координат, стрелка вектора — указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
Радиус-вектор точки — это вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат
Ра́диус-ве́ктор (обычно обозначается 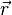 или просто
или просто 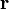 ) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки , называемой началомкоординат.
) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки , называемой началомкоординат.
Скорость – это векторная физическая величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Мгновенная скорость материальной точки – это средняя скорость за бесконечно малый интервал времени, определяемая как векторная величина, равная первой производной по времени от радиус-вектора rрассматриваемой точки:
v=lim(∆t→0) ∆r/∆t=dr/dt=r’ Вектор мгновенной скорости направлен по касательной к траектории в сторону движения.
Кинематический закон движения– это функция, выражающая положение точки в любой момент времени: r = r(t) (2.1)
Уравнение (2.1) является векторной формой закона. Движение материальной точки полностью определено, если координаты материальной точки заданы в зависимости от времени: x = x(t), y = y(t), z = z(t) . (2.2)
Траектория– это кривая, которую описывает радиус-вектор r(t) координат материальной точки (или тела) с течением времени.
Вектор перемещения∆r = r — r – это вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени):
∆r = r — r = r(t) — r(t) . В пределе ∆t→0 модуль элементарного перемещения равен элементарному пути: |dr| =ds .
Вектор угловой скорости w характеризует быстроту изменения угла поворота и определяется как
w =d(фи)/dt (2.15) где dt – промежуток времени, за которое тело совершает поворот d(фи) ; w =|фи’|.
Единицаугловой скорости в СИ – радиан на секунду (рад/с).
Аксиальные векторы– это векторы, направление которых связывают с направлением вращения. Начало вектора w можно совместить с любой точкой, принадлежащей оси вращения. Вектор w совпадает с наравлением вектора w и является аксиальным вектором.
Изменение вектора wсо временем характеризуют вектором углового ускорения(бета):
(бета)=dw/dt=w’=d 2 (фи’)/dt2 .Единицауглового ускорения в СИ – радиан на секунду в квадрате (рад/с 2 ).
Равномерное вращение характеризуется периодом вращенияТ – временем, за которое точка совершает один полный оборот: T=2П/w.
Частота вращения– число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени: n=1/T=w/2П.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8946 —  | 7616 —
| 7616 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Основные формулы кинематики материальной точки
Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.
Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .
Скорость точки:
;
.
.
Единичный вектор в направлении касательной к траектории точки:
.
Тангенциальное (касательное) ускорение:
;
;
.
Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.
Радиус кривизны траектории:
.
Далее приводится вывод этих формул и изложение теории кинематики материальной точки.
Радиус-вектор и траектория точки
Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.
Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .
При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.
Траектория материальной точки – это линия, вдоль которой происходит движение точки.
Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями
В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .
Скорость материальной точки
Согласно определению скорости и определению производной:
Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:
,
где
,
,
– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.
Таким образом
.
Модуль скорости:
.
Касательная к траектории
С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.
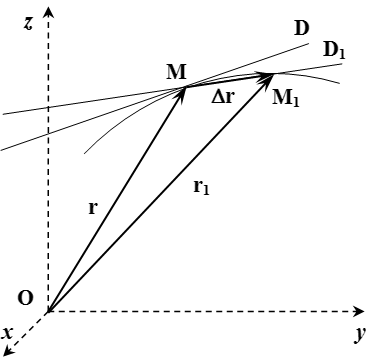
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .
При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.
Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.
Тогда вектор скорости точки можно представить в виде:
.
Далее мы считаем, что если над буквой векторной величины не стоит стрелка, то это обозначает модуль вектора.
Ускорение материальной точки
Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.
Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают скалярное произведение векторов. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.
Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к касательной.
Тангенциальное (касательное) ускорение
Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили:
.
Отсюда видно, что тангенциальное ускорение равно проекции полного ускорения на направление касательной к траектории или, что тоже самое, на направление скорости точки.
Тангенциальное (касательное) ускорение материальной точки – это проекция ее полного ускорения на направление касательной к траектории (или на направление скорости).
Символом мы обозначаем вектор тангенциального ускорения, направленный вдоль касательной к траектории. Тогда – это скалярная величина, равная проекции полного ускорения на направление касательной. Она может быть как положительной, так и отрицательной.
Подставим в формулу:
.
Тогда:
.
То есть тангенциальное ускорение равно производной по времени от модуля скорости точки. Таким образом, тангенциальное ускорение приводит к изменению абсолютной величины скорости точки. При увеличении скорости, тангенциальное ускорение положительно (или направлено вдоль скорости). При уменьшении скорости, тангенциальное ускорение отрицательно (или направлено противоположно скорости).
Радиус кривизны траектории
Теперь исследуем вектор .
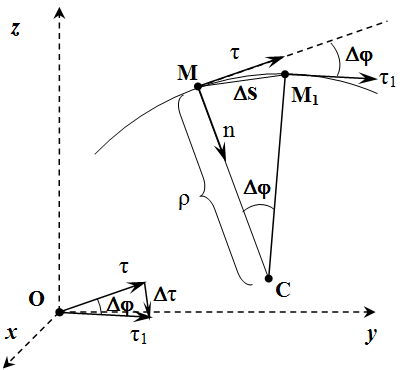
Рассмотрим единичный вектор касательной к траектории . Поместим его начало в начало системы координат. Тогда конец вектора будет находиться на сфере единичного радиуса. При движении материальной точки, конец вектора будет перемещаться по этой сфере. То есть он будет вращаться вокруг своего начала. Пусть – мгновенная угловая скорость вращения вектора в момент времени . Тогда его производная – это скорость движения конца вектора. Она направлена перпендикулярно вектору . Применим формулу для вращающегося движения. Модуль вектора:
.
Теперь рассмотрим положение точки для двух близких моментов времени. Пусть в момент времени точка находится в положении , а в момент времени – в положении . Пусть и – единичные векторы, направленные по касательной к траектории в этих точках. Через точки и проведем плоскости, перпендикулярные векторам и . Пусть – это прямая, образованная пересечением этих плоскостей. Из точки опустим перпендикуляр на прямую . Если положения точек и достаточно близки, то движение точки можно рассматривать как вращение по окружности радиуса вокруг оси , которая будет мгновенной осью вращения материальной точки. Поскольку векторы и перпендикулярны плоскостям и , то угол между этими плоскостями равен углу между векторами и . Тогда мгновенная скорость вращения точки вокруг оси равна мгновенной скорости вращения вектора :
.
Здесь – расстояние между точками и .
Таким образом мы нашли модуль производной по времени вектора :
.
Как мы указали ранее, вектор перпендикулярен вектору . Из приведенных рассуждений видно, что он направлен в сторону мгновенного центра кривизны траектории. Такое направление называется главной нормалью.
Нормальное ускорение
Нормальное ускорение
направлено вдоль вектора . Как мы выяснили, этот вектор направлен перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.
Пусть – единичный вектор, направленный от материальной точки к мгновенному центру кривизны траектории (вдоль главной нормали). Тогда
;
.
Поскольку оба вектора и имеют одинаковое направление – к центру кривизны траектории, то
.
Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.
Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.
Нормальное ускорение материальной точки – это проекция ее полного ускорения на направление, перпендикулярное к касательной к траектории.
Подставим . Тогда
.
То есть нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.
Отсюда можно найти радиус кривизны траектории:
.
И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.
Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.
Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 19-02-2016


