В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода радиус его орбиты и период обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус орбиты | Период обращения вокруг Земли |
Центростремительное ускорение рассчитывается по формуле: При движении по орбите центростремительное ускорение возникает вследствие гравитационного взаимодействия с Землёй:
где
и
— массы спутника и Земли соответственно. При уменьшении центростремительного ускорения радиус обращения увеличивается. Из приведённых формул получим, что
заметим, что при удалении от Земли скорость спутника уменьшается. Период обращения — это время за которое спутник делает полный оборот вокруг Земли, то есть
Следовательно, период обращения спутника увеличится.
Можно заметить, что раз радиус обращения увеличивается, а скорость обращения падает, то период обращения увеличивается.
При движении спутников (с выключенным двигателем) по круговой орбите на них действует только одна сила — сила притяжения спутника к планете.
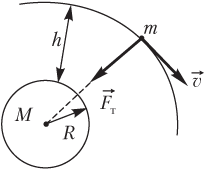
На спутник, имеющий массу m и движущийся по круговой орбите на высоте h над поверхностью планеты (рис. 2.2), действует только сила тяжести.
Эта сила направлена к центру планеты и сообщает спутнику центростремительное ускорение. В этом случае справедливо соотношение
G m M r 2 = m v 2 r ,
позволяющее получить формулу для расчета первой космической скорости спутника:
где G = 6,67 ⋅ 10 −11 Н ⋅ м 2 /кг 2 — универсальная гравитационная постоянная; m — масса тела; r = R + h — радиус орбиты; R — радиус планеты; h — высота спутника над поверхностью планеты.
Различают первую, вторую и третью космические скорости. Для планеты Земля:
- первая космическая скорость — минимальная скорость, сообщенная спутнику вблизи поверхности Земли, при которой он может выйти на круговую орбиту и начать вращение вокруг Земли на околоземной орбите ( h ≈ 0),
- вторая космическая скорость — минимальная скорость, сообщенная спутнику вблизи поверхности Земли, при которой он может удалиться от Земли на большое расстояние и стать спутником Солнца,
- третья космическая скорость — минимальная скорость, сообщенная спутнику вблизи поверхности Земли, при которой он может покинуть Солнечную систему; ее значение приблизительно равно 16,6 км/с.
Когда говорят о первой космической скорости для планеты , то подразумевают, что спутник движется на высоте h ≈ 0, т.е. радиус орбиты спутника r совпадает с радиусом планеты R :
Период обращения спутника вокруг планеты (время одного оборота) можно определить как отношение длины орбиты к первой космической скорости:
где L = 2π r — длина орбиты радиусом r (длина окружности); v — первая космическая скорость спутника на этой орбите.
Пример 5. Во сколько раз период обращения искусственного спутника, совершающего движение по круговой орбите на высоте, равной удвоенному радиусу Земли, превышает период обращения спутника, вращающегося на околоземной орбите?
Решение. Период обращения спутника, совершающего движение по круговой орбите на высоте h 1 = 2 R , определяется формулой
T 1 = 2 π ( R + h 1 ) v 1 ,
где R — радиус Земли; v 1 — первая космическая скорость спутника на высоте h 1 .
Период обращения спутника, совершающего движение на околоземной орбите ( h 2 ≈ 0), определяется формулой
T 2 = 2 π ( R + h 2 ) v 2 ,
где v 2 — первая космическая скорость спутника на околоземной орбите.
Подстановка значений h 1 = 2 R и h 2 = 0 в формулы для вычисления соответствующих периодов дает:
T 1 = 6 π R v 1 и T 2 = 2 π R v 2 .
T 1 T 2 = 3 v 2 v 1
выражается через отношение первых космических скоростей спутника на соответствующих орбитах.
Первые космические скорости определяются следующими формулами:
v 1 = G M R + h 1 = G M R + 2 R = G M 3 R ;
- для высоты h 2 ≈ 0 (околоземная орбита)
v 2 = G M R + h 2 = G M R + 0 = G M R ,
где G = 6,67 ⋅ 10 −11 Н · м 2 /кг 2 — универсальная гравитационная постоянная; M — масса Земли.
Подставляя v 1 и v 2 в формулу для отношения периодов, получим
T 1 T 2 = 3 v 2 v 1 = 3 G M R ⋅ 3 R G M = 3 3 ≈ 5,2 .
т.е. период обращения спутника, совершающего движение на высоте, равной двум радиусам, превышает период обращения спутника на околоземной орбите приблизительно в 5,2 раза.
Пример 6. Радиус некоторой планеты в 3 раза больше радиуса Земли, а плотность в 9 раз меньше плотности Земли. Определить отношение первых космических скоростей спутников для Земли и для планеты.
Решение. Сравниваются следующие первые космические скорости:
- для поверхности планеты
где G = 6,67 ⋅ 10 −11 Н · м 2 /кг 2 — универсальная гравитационная постоянная; M З — масса Земли; R З — радиус Земли; M — масса планеты; R — радиус планеты.
Отношение скоростей равно
v 1 v 2 = M З R З R M .
Считая, что Земля и планета имеют шарообразную форму, получим формулы для вычисления соответствующих масс:
M З = ρ З V З = 4 3 π ρ З R З 3 ,
M = ρ V = 4 3 π ρ R 3 ,
где ρ З — плотность Земли; ρ — плотность планеты.
Подставим выражения для масс в формулу для отношения скоростей:
v 1 v 2 = 4 3 π ρ З R З 3 R З 3 4 R π ρ R 3 = ρ З R З 2 ρ R 2 = R З R ρ З ρ .
По условию задачи R = 3 R З и ρ З = 9ρ; следовательно, искомое отношение скоростей равно
v 1 v 2 = R З 3 R З 9 ρ ρ = 1 ,
т.е. скорости спутника одинаковы для поверхности Земли и для поверхности планеты.
Пример 7. Вокруг некоторой планеты по круговой орбите радиусом 20 000 км вращается спутник со скоростью 12 км/с. Определить величину ускорения свободного падения на поверхности планеты, если ее радиус равен 12 000 км.
Решение. Ускорение свободного падения на поверхности планеты найдем по формуле
где G = 6,67 ⋅ 10 −11 Н · м 2 /кг 2 — универсальная гравитационная постоянная; M — масса планеты; R — радиус планеты.
Радиус планеты задан в условии задачи, произведение ( GM ) можно выразить из формулы для первой космической скорости:
v = G M R + h = G M r ,
где r — радиус орбиты спутника; отсюда искомое произведение
Подставим ( GM ) в выражение для вычисления g 0 :
Расчет позволяет получить значение ускорения свободного падения на поверхности планеты:
g 0 = ( 12 ⋅ 10 3 ) 2 ⋅ 2, 0 ⋅ 10 7 ( 12 ⋅ 10 6 ) 2 = 20 м/с 2 .
Дано: Rз = 6,371·10⁶м — радиус Земли
Н = 6·10⁵м — высота спутника над поверхностью Земли
G = 6,6742·10−11 м³с−2кг−1 — гравитационная постоянная
Мз = 5,9736·10²⁴ кг — масса Земли
Найти: 1) v — cкорость спутника
2) Т — период обращения спутника вокруг Земли
1) Найдём ускорение свободного падения на высоте Н:
= 5,9736·10²⁴ · 6,6742·10−11 /(6,371·10⁶ + 6·10⁵ ) =
2) Найдём скорость спутника из формулы а = g = v²/(Rз +Н)
3) Найдём период обращения спутника вокруг Земли:
Ответ: v = 7562 км/с, T ≈ 1час 36мин
На ИСЗ действуют центробежная сила и сила притяжения Земли, при их равенстве спутник будет вращаться по круговой орбите.
V²=γ*M/(R+h), где R=6,4*10^6м, h=6*10^5м, M=6*10^24кг, γ=6,67*10^(-11)м³/кг*с²
V = √6,67*10^(-11)*6*10^24/(6,4*10^6+6*10^5)=√57,17*10^6= 7,6*10^3 м/с
Период определим, разделив длину окружности на скорость
Т = 2π(R+h)/V = 2π*7*10^6/7,6*10^3 = 1,8π*10³ c = π/2 час