Содержание
| Земля | 9,81 м/с 2 | 1,00 g | Солнце | 273,1 м/с 2 | 27,85 g |
| Луна | 1,62 м/с 2 | 0,165 g | Меркурий | 3,68—3,74 м/с 2 | 0,375—0,381 g |
| Венера | 8,88 м/с 2 | 0,906 g | Марс | 3,86 м/с 2 | 0,394 g |
| Юпитер | 23,95 м/с 2 | 2,442 g | Сатурн | 10,44 м/с 2 | 1,065 g |
| Уран | 8,86 м/с 2 | 0,903 g | Нептун | 11,09 м/с 2 | 1,131 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил. В соответствии с уравнением движения тел в неинерциальных системах отсчёта [2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах [3] . Стандартное («нормальное») значение, принятое при построении систем единиц, составляет g = 9,80666 м/с² [4] [5] . Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или, грубо, 10 м/с².
Содержание
Физическая сущность [ править | править код ]
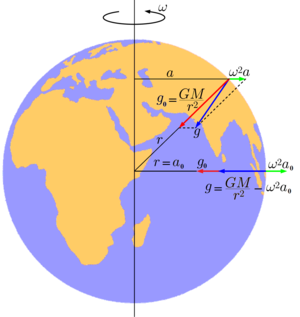
Для определённости будем считать, что речь идёт об ускорении свободного падения на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центростремительного ускорения, связанного с вращением Земли.
Центростремительное ускорение [ править | править код ]
Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, центростремительное ускорение равно ω 2 a , где ω — угловая скорость вращения Земли, определяемая выражением ω = 2π/T , в котором Т — время одного оборота вокруг своей оси (звёздные сутки), равное для Земли 86164 секунды. Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с 2 , причем на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение [ править | править код ]
| h , км | g, м/с 2 | h , км | g, м/с 2 |
|---|---|---|---|
| 9,8066 | 20 | 9,7452 | |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связано с его массой M следующим соотношением:
g = G M r 2 <displaystyle g=G<frac 
где G — гравитационная постоянная (6,67408(31)·10 −11 м 3 ·с −2 ·кг −1 ) [6] , а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрично. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо наоборот по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
g ( h ) = G M ( r + h ) 2 <displaystyle g(h)=<frac 
Ускорение свободного падения на Земле [ править | править код ]
Ускорение свободного падения у поверхности Земли зависит от широты, времени суток, атмосферного давления и других факторов. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле [7] [8] :
g = 9,780 318 ( 1 + 0,005 302 sin 2 φ − 0,000 006 sin 2 2 φ ) − 0,000 003086 h , <displaystyle g=9<,>780318(1+0<,>005302sin ^<2>varphi -0<,>000006sin ^<2>2varphi )-0<,>000003086h,> 


Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли, дополнив её поправками, связанными с вращением Земли, приливными воздействиями и другими факторами.
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счет центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от следствий из этой упрощённой модели. Так, самое низкое значение g зафиксировано на горе Уаскаран в Перу (9,7639 м/с²) в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от северного полюса [9] .
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с 2 |
| Алматы | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение [ править | править код ]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
На стыке XVII и XVIII веков жил в Британии один ученый, Исаак Ньютон, отличавшийся большой наблюдательностью. Так случилось, что вид сада, где с веток на землю падали яблоки, помог ему открыть закон всемирного тяготения. Какая же сила заставляет плод все быстрее двигаться к поверхности планеты, по каким законам происходит это перемещение? Попытаемся ответить на эти вопросы.
А если бы эти яблони, как обещала в свое время советская пропаганда, росли на Марсе, каким бы тогда было это падение? Ускорение свободного падения на Марсе, на нашей планете, на других телах Солнечной системы. От чего оно зависит, каких величин достигает?
Ускорение свободного падения
Чем замечательна знаменитая Пизанская башня? Наклоном, архитектурой? Да. А еще с нее удобно бросать вниз различные предметы, чем и занимался в начале XVII века знаменитый итальянский исследователь Галилео Галилей. Бросая вниз всякие вещицы, он заметил, что тяжелый шар в первые мгновения падения двигается медленно, затем скорость его возрастает. Исследователя интересовал математический закон, по которому происходит изменение скорости.
Измерения, произведенные в дальнейшем, в том числе другими исследователями, показали, что скорость падающего тела:
- за 1 секунду падения становится равной 9,8 м/с;
- за 2 секунды – 19,6 м/с;
- 3 – 29,4 м/с;
- …
- n секунд – n∙9,8 м/с.
Эта величина 9,8 м/с∙с получила название «ускорение свободного падения». На Марсе (Красной планете) или другой планете это ускорение такое же или нет?
Почему на Марсе по-другому
Исаак Ньютон, рассказавший миру, что такое всемирное тяготение, смог сформулировать и закон ускорения свободного падения.

С развитием технологий, поднявших на новый уровень точность лабораторных измерений, ученые смогли подтвердить, что ускорение свободного падения на планете Земля – не такая уж и постоянная величина. Так, на полюсах она больше, на экваторе – меньше.
Ответ на эту загадку кроется в вышеуказанном уравнении. Дело в том, что земной шар, строго говоря, не совсем шар. Это эллипсоид, слегка приплюснутый с полюсов. Расстояние до центра планеты на полюсах меньше. А уж как отличается и массой, и размерами от земного шара Марс. Ускорение свободного падения на нем также будет иным.
Используя уравнение Ньютона и общеизвестные данные:
- масса планеты Марс − 6,4171·10 23 кг;
- средний диаметр − 3389500 м;
- гравитационная константа − 6,67∙10 -11 м 3 ∙с -2 ∙кг -1 .
Не составит труда найти ускорение свободного падения на Марсе.

g Марса = 6,67∙10 -11 ∙6,4171·10 23 / 3389500 2 = 3,71 м/с 2 .
Для проверки полученного значения можно заглянуть в любой справочник. Оно совпадает с табличным, значит, расчет произведен правильно.
Как ускорение свободного падения связано с весом
Вес – это сила, с которой любое тело, обладающее массой, давит на поверхность планеты. Измеряется он в ньютонах и равен произведению массы на ускорение свободного падения. На Марсе и любой другой планете оно, разумеется, будет отличаться от земного. Так, на Луне сила тяжести в шесть раз меньше, чем на поверхности нашей планеты. Это даже создавало определенные трудности у астронавтов, высадившихся на естественный спутник. Перемещаться оказалось удобнее, подражая кенгуру.

Итак, как было рассчитано, ускорение свободного падения на Марсе составляет 3,7 м/с 2 , или 3,7 / 9,8 = 0,38 от земного.
А означает это, что вес любого предмета на поверхности Красной планеты будет составлять лишь 38% от веса этого же предмета на Земле.
Как и где это работает
Попутешествуем мысленно по Вселенной и найдем ускорение свободного падения на планетах и других космических телах. Астронавты НАСА планируют уже в течение ближайших десятилетий высадиться на одном из астероидов. Возьмем Весту – самый большой астероид в Солнечной системе (Церера была побольше, но ее недавно перевели в разряд карликовых планет, «повысили в звании»).

g Весты = 0,22 м/с 2 .
Все массивные тела станут легче в 45 раз. При такой маленькой гравитации проблемой станут любые работы на поверхности. Неосторожный рывок или прыжок сразу подбросит астронавта на несколько десятков метров вверх. Что уж говорить про планы по добыче на астероидах полезных ископаемых. Экскаватор или бурильную установку придется в прямом смысле слова привязывать к этим космическим скалам.
А теперь другая крайность. Представим себя на поверхности нейтронной звезды (тело с массой солнца, имеющее при этом диаметр около 15 км). Так вот, если каким-то непостижимым образом астронавт не погибнет от зашкаливающего радиационного излучения всех возможных диапазонов, то его взору предстанет следующая картина:
g н.звезды = 6,67∙10 -11 ∙1,9885·10 30 / 7500 2 = 2 357 919 111 111 м/с 2 .

Монетка массой в 1 грамм весила бы на поверхности этого уникального космического объекта 240 тысяч тонн.
Прежде чем рассказать, какое ускорение свободного падения на Марсе, нужно немного описать планету и её характеристики.
Красная планета — четвертая от Солнца. Его радиус составляет около половины радиуса Земли. А масса около десятой части массы нашей планеты. В числовых значениях это: R=3389,5 км; масса=6,42×10²³.
УСП — это ускорение, придаваемое телу силой тяжести, при исключении влияния на это же тело других сил. То есть если бросить предмет вниз, просто отпустив его, то ускорение, с которым он полетит к поверхности — это и будет искомое значение.
Зная вес и радиус любого небесного тела, несложно рассчитать нужное значение.
Формула для такого расчета выглядит следующим образом:
g = G•M/(R + H)²
G — неизменная величина гравитации 6,674210 –¹¹
М — вес
R — радиус
h — расстояние от поверхности планеты до тела (ускорение которого надо рассчитать).
Если в формулу подставить параметры Марса, то ускорение свободного падения на Марсе получится 3,86 м/с².
Стоит заметить, что на результат расчетов могут повлиять плотность атмосферы и сила ветра. Поэтому, если необходимо точные данные, то его нужно рассчитывать в каждом индивидуальном случае, учитывая мельчайшие параметры.
Если сравнивать с нашей планетой, то на Земле УСП в 2,5 раза больше.
Мы постарались рассказать вам очень кратко и понятно, если вдруг, вам что-то неясно, то пишите в комментариях вопросы, мы вам всё подробно расскажем.


