 Что такое теорема о трех перпендикулярах простыми словами
Что такое теорема о трех перпендикулярах простыми словами
Как ее использовать в задачах
Как оформлять на ЕГЭ
Начнем с парочки вводных понятий, ты же хочешь жить по понятиям?
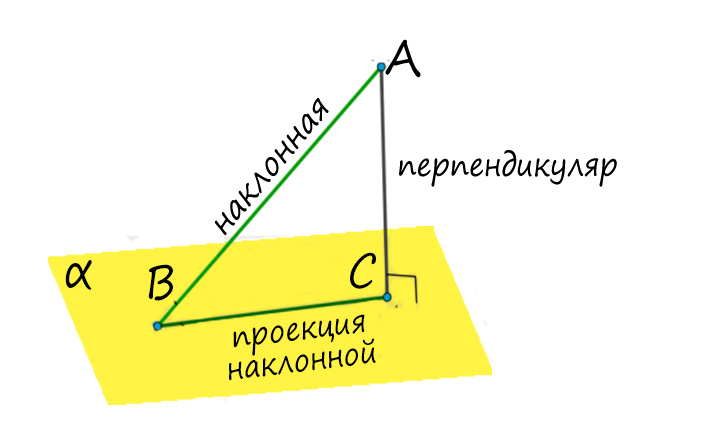
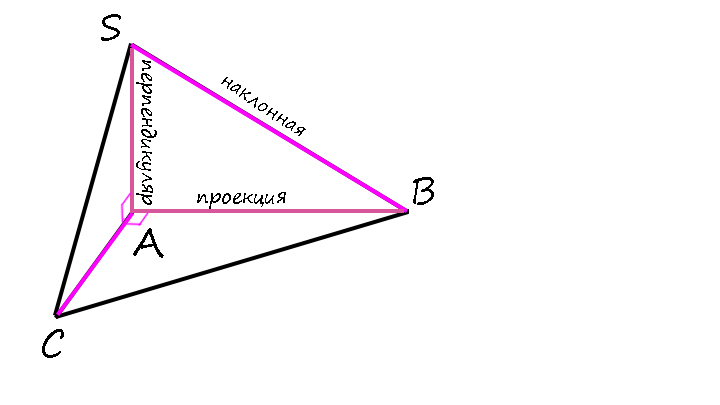
Если в плоскости альфа провести прямую KL через точку В так, что KL ⊥ BC, тогда по теореме о трех перпендикулярах (т.т.п.) KL ⊥ BA.
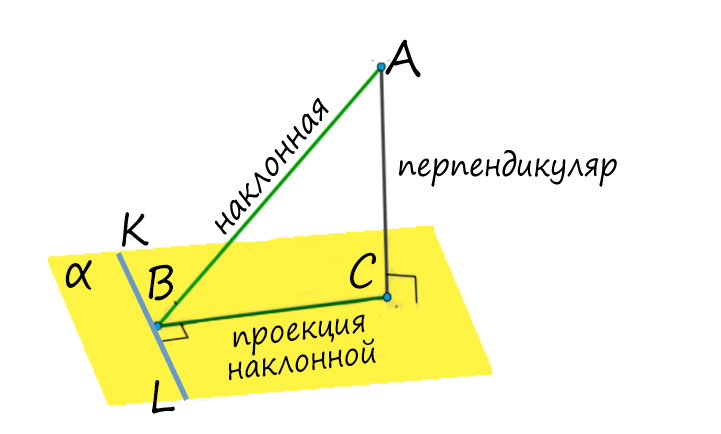
Словами можно сказать так: прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость (верно и наоборот).
Перейдем к самому распространенному примеру:
1) Докажите, что в тетраэдре скрещивающиеся ребра перпендикулярны.
У тетраэдра есть три пары скрещивающихся ребер. Докажем перпендикулярность одной пары, другие вы сделаете по аналогии, например, AD ⊥ BC.
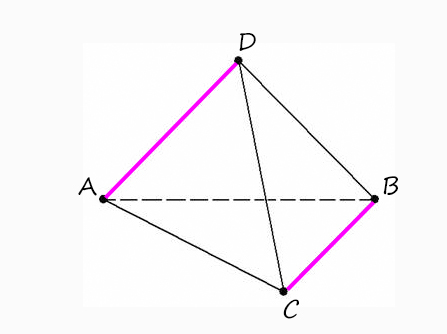
Сейчас есть только наклонная AD и плоскость (ABC), значит, нам не хватает проекции наклонной и перпендикуляра, тогда проведем их:
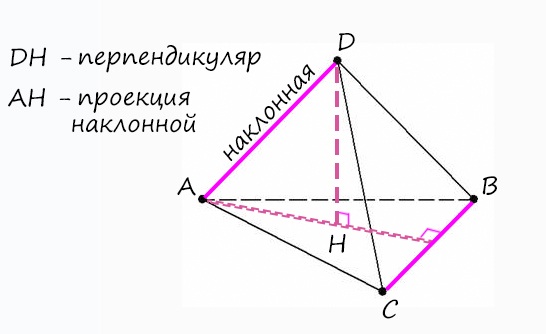
Тогда, чтобы доказать, что AD ⊥ BC:
1) AH ⊥ BC (если продлить АН до пересечения с BC), т.к. AH является выстой в правильном треугольнике.
2) DH ⊥ (ABC) (по построению, а, значит, перпендикулярно любой прямой, находящейся в этой плоскости) => DH ⊥ BC.
После того, как мы это доказали, можем смело сказать, что AD ⊥ BC (всегда дожно быть доказательство двух пунктов, и только тогда вывод).
2) Докажите, что в прямом параллепипеде ребра B₁C и CD перпендикулярны.
Возьмем B₁C как наклонную к плоскости (ABCD), тогда перпендикуляром будет BB₁, а проекцией наклонной на эту плоскость — BC.
1) BB₁ ⊥ (ABCD) т.к. параллепипед прямой (боковые ребра перпендикулярны плоскости основания) => BB₁ ⊥ CD (если прямая перпендикулярна плоскости, то и перпендикулярна всем прямым, лежащим в этой плоскости).
2) BC ⊥ CD т.к. ABCD — прямоугольник.
3) По т.т.п.: B₁C ⊥ CD.
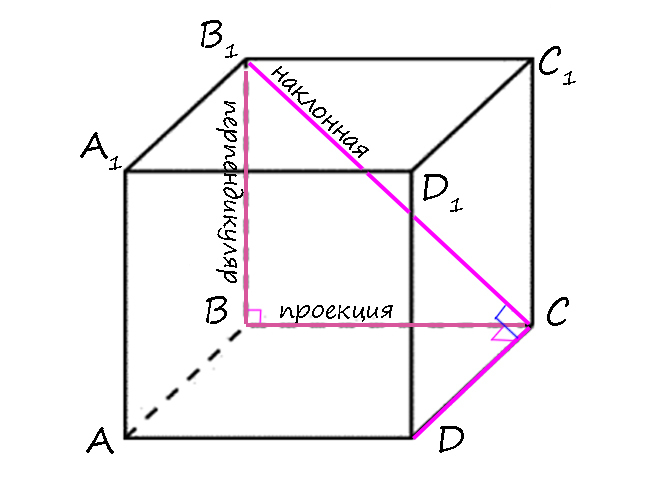
Два пункта доказательства, третий пункт вывод.
3) Дана пирамида SABC с высотой AS, в основании которой лежит прямоугольный треугольник с прямым углом A. Докажите, что SB⊥ AC.
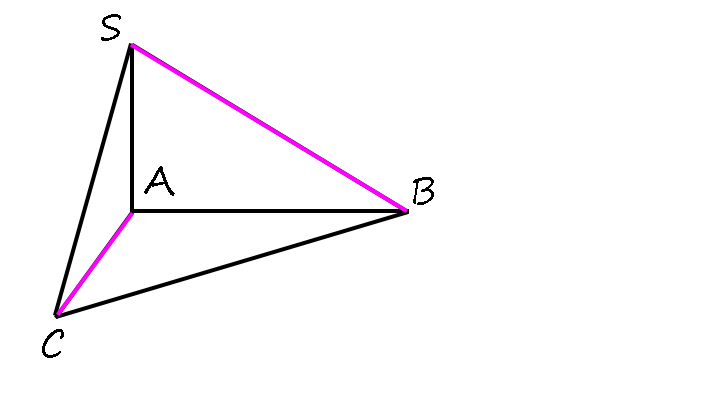
Скажем, что BC — наклонная к плоскости (ABC):
1) SA ⊥ (ABC) => SA ⊥ AC
2) AB ⊥ AC ( ABC — прямоугольный треугольник по условию).
3) По т.т.п.: SB ⊥ AC.
 Вывод:
Вывод:
Два пункта доказательство и вывод!
1) Перпендикуляр будет опускаться на плоскость под 90 °.
2) Проекция наклонной на плоскость перпендикулярна прямой.
3) По т.т.п. наклонная перпендикулярна прямой.
Привет. Прям на первом вопросе впал в ступор(((
Назовите все пары скрещивающихся (т. е. принадлежащих скрещивающимся прямым) ребер тетраэдра АВСD. Сколько таких пар ребер имеет тетраэдр?
Рекомендации к решению№260, №261,С2 ЕГЭ — 2011Методическая разработкаучителя Поляковой Е. А.
В правильной треугольной пирамиде DABCчерез боковое ребро DС и высоту DO пирамидыпроведена плоскость α.Докажите, что ребро АBперпендикулярно к плоскости α 1) ∆АBС — __________________, тогда2) О – центр вписанной в ∆АBС окружности 3) СМ — __________ и высота ∆АBС , значит, 4) АВ лежит в плоскости АBС, DO ___ АВС, тогда 5) Оказалось, что АВ перпендикуляр к СМ и к DO, значит, АВ — перпендикуляр к плоскости DСM, причёмплоскость DСM совпадает с плоскостью α 5) ∆ DСM – сечение пирамиды плоскостью α, тогда ребро АB перпендикулярно к плоскости DСM, значит, и к плоскости α
Свойство скрещивающихся рёбер правильной треугольной пирамиды
Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра взаимно перпендикулярныДоказательство.1) Докажем, что перпендикулярны ребра АВ и CD2) через боковое ребро DС и высоту DO пирамиды проведём плоскость α3) ∆ DСM – сечение пирамиды плоскостью α, тогда ребро АBперпендикулярно к плоскости DСM (по задаче №260), значит, и к ребру CD, лежащему в этой плоскости, т. е. перпендикулярны ребра АВ и CD.Аналогично докажем, что перпендикулярны ребра АС и DВ;ВС и AD5) Так же можно провести доказательство перпендикулярности пары рёбер ВС и AD
Применение свойства скрещивающихся рёбер правильной треугольной пирамиды в задаче С2 ЕГЭ — 2011
Дана правильная треугольная пирамида DABC с вершиной DРебро основания пирамиды равноа высота равна Найдите расстояние от середины ребра DB до прямой МТ, где М и Т — середины рёбер АС и АВ соответственно.Решение с рекомендациями1). М и Т — середины рёбер АС и АВ,тогда МТ – _______ ___________ ∆АВС. 2). Проведём KN║ МТ3). KNМТ — _________________, точнее – прямоугольник, так как4). Скрещивающиеся рёбра правильной треугольной пирамиды _________ ______________(см. решение №261, геометрия 10 — 11)5). AD ____ ВС, тогда MN ____ KN или КТ ____ МТ,т. е. КТ – искомое расстояниеКТ – ________ _____________ ∆АВD,
6) О – центр вписанной в ∆АBС окружности, АР — __________ и высота ∆АBС , значит, ∆АPС — ____________________ и АР = АС ∙ sin 60° = _____ = ____ катет, противолежащий углу, равен произведению гипотенузы на синус этого угла7) По свойству медиан треугольника: АО = ___ АР = 8) ∆АOD — ____________________ ипо теореме Пифагора AD = Тогда КТ = Ответ:


