Существует и другой способ геометрической интерпретации комплексных чисел. Каждой точке (x , y) координатной плоскости, изображающей комплексное число
z = x + yi, соответствует единственный вектор, отложенный от начала системы координат и обратно (рис. 5). При этом двум различным точкам координатной плоскости будут соответствовать два таких различных вектора.
Таким образом, может быть установлено взаимно однозначное соответствие между множеством точек координатной плоскости (комплексными числами) и множеством векторов, отложенных от начала системы координат.
Если z = x + yi (рис. 5), то вектор 
, отложенный от начала системы координат до точки, изображающей число z, будет иметь координаты (x; y). Известно, что равные векторы имеют равные координаты.
Итак, мы рассмотрели два способа интерпретации комплексных чисел: их можно изображать либо точками координатной плоскости, либо векторами, отложенными от начала системы координат. При этом любые два равных вектора (имеющих одно и то же направление и равные длины) изображают одно и то же комплексное число, а векторы, отличные либо длиной, либо направлением, изображают разные числа. На рисунке 6 с помощью векторов изображены различные комплексные числа: 
изображает число 2 + 0i;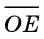 
– число – 3 + 0i; – число 0 + i; 
– число 0 + 2i; 
– число 0 – 3i; 
– число 3 + 2i; 
– число – 1 – 2i.
Ясно, что любой ненулевой вектор, лежащий на оси Oy (или параллельный ей), изображает чисто мнимое число yi, причем y > 0, если направление вектора совпадает с направлением оси, y
Тогда произведение данных комплексных чисел равно комплексному числу:
Последнее соотношение позволяет сформулировать правило умножения комплексных чисел: при умножении двух комплексных чисел их модули перемножаются, а их аргументы складываются. Это проиллюстрировано на рисунке 8.
Ясно, что произведение комплексных чисел связано с поворотом (вращением). Так, произведение z1z2 изображается вектором представляющим собой образ вектора 
, повернутого на угол j2 (или образ вектора 
, повернутого на угол j1), при этом модуль вектора равен произведению модулей данных векторов.
Связь произведения комплексных чисел с вращением становится более наглядной, если рассматривать произведение различных комплексных чисел (векторов) на комплексное число i, у которого модуль равен 1, а аргумент 90°. Например, найдем произведение комплексных чисел z1 = 1 + i и z2 = i.
z = z1z2 = (1 + i)i = i + i 2 = – 1 + i.
Числа z1 и z2 соответственно изображают векторы и (рис.9). Мы видим, что модуль комплексного числа z равен модулю числа z1:
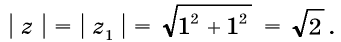
Аргумент же комплексного числа z равен 45° + 90° = 135°, в то время, как аргумент комплексного числа z1 равен 45°. Т.е. вектор , изображающий число z, есть образ вектора , изображающего число z1 при повороте на 90°.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: "Что-то тут концом пахнет". 8517 — 
| 8103 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Мы рассмотрели, как можно изобразить неподвижным вектором любую синусоидальную функцию времени. Рассмотрим теперь способ изображения вектора комплексным числом.
Возьмем прямоугольную систему координат (рис. 5.3) и условимся откладывать по горизонтальной оси вещественные числа, а по вертикальной оси — мнимые числа. Совместим начало вектора с началом координат. Конец вектора окажется совмещенным с некоторой точкой на плоскости. Этой точке соответствует определенное комплексное число. Следовательно, заданному вектору соответствует единственное комплексное число. Так, например, на рис. 5.3 вектору / соответствует точка Afj, вектору U соответствует точка М.г
Любой вектор в комплексной плоскости изображается отрезком, длина которого в определенном масштабе выражает модуль вектора. Направление вектора определяется углом, отсчитываемым от положительного направления оси действительных величин. Если угол отсчитывается против часовой стрелки, он берется со знаком плюс. Если угол отсчитывается в направлении вращения часовой стрелки, он берется со знаком минус.
Рассмотрим различные формы записи комплексного числа. Действительная часть а комплексного числа откладывается по оси действительных величин, коэффициент b при мнимой части — по оси мнимых величин.
Вектор Л (рис. 5.4) изображается комплексным числом
Это выражение называют алгебраической формой записи комплексного числа.
На основании рис. 5.4 можно записать 
Следовательно, 
Это выражение называют тригонометрической формой записи комплексного числа. Здесь А — модуль комплексного числа — находится по теореме Пифагора:
а угол а определяется по его тангенсу:
По формуле Эйлера
где е — основание натуральных логарифмов.
Используя это равенство, представим комплексное число в показательной форме:
Таким образом, 
УСЛОВИЕ:
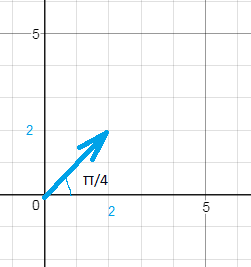
Изобразить векторами и записать в тригонометрической и показательной формах комплексное число z=2+2i
РЕШЕНИЕ ОТ sova ✪ ЛУЧШЕЕ РЕШЕНИЕ
|z|=sqrt(2^2+2^2)=sqrt(4+4)=sqrt(8)=2sqrt(2);
cosφ = x/|z| = 1/sqrt(2)
sinφ = y/z = 1/ sqrt(2)
φ=π/4
z=2sqrt(2)*(cos(π/4) + i*sin(π/4))- триг форма
z=2*e^(i(π/4)) — показ форма
Добавил alekseevadaria , просмотры: ☺ 653 ⌚ 2018-11-12 17:51:45. математика 2k класс
Решения пользователей
Написать комментарий
Поиск в массиве осуществляй с помощью .find
Даллее конкотинируешь слово привет из объекта с именем
Решают либо методом Бернулли, либо методом вариации произвольной постоянной:
Метод Бернулли.
Ищут решение y в виде произведения u*v
Уравнение принимает вид:
Выносим за скобки u:
Так как функции u и v — произвольные, то выбираем их так, чтобы
v`-frac<2x-5>v=0
тогда
u`*v =5
Осталось решить два уравнения с разделяющимися переменными
Интегрируем, при этом С=0
int frac
Решаем второе уравнение
y=x^2+C*x^2*e^(frac<5>
Подставляем вместо х=2;вместо y=4
находим С и получаем частное решение
Загрузка...
