В системе MatLab достаточно просто выполняются математические операции над матрицами и векторами. Рассмотрим сначала простые операции сложения и умножения матриц и векторов. Пусть даны два вектора
a = [1 2 3 4 5]; % вектор-строка
b = [1; 1; 1; 1; 1]; % вектор-столбец
тогда умножение этих двух векторов можно записать так
c = a*b; % c=1+2+3+4+5=16
d = b*a; % d – матрица 5х5 элементов
В соответствии с операциями над векторами, умножение вектор-строки на вектор-столбец дает число, а умножение вектор-столбца на вектор-строку дает двумерную матрицу, что и является результатом вычислений в приведенном примере, т.е.


Сложение и вычитание двух векторов записывается так
a1 = [1 2 3 4 5];
a2 = [5 4 3 2 1];
c = a1+a2; % c = [1+5, 2+4, 3+3, 4+2, 5+1];
с = a2-a1; % c = [5-1, 4-2, 3-3, 2-4, 1-5];
Следует обратить внимание, что операции сложения и вычитания можно выполнять между двумя векторами-столбцами или двумя векторами-строками. Иначе MatLab выдаст сообщение об ошибке, т.к. разнотипные векторы складывать нельзя. Так обстоит дело со всеми недопустимыми арифметическими операциями: в случае невозможности их вычисления система MatLab сообщит об ошибке и выполнение программы будет завершено на соответствующей строке.
Аналогичным образом выполняются операции умножения и сложения между матрицами:
A = [1 2 3; 4 5 6; 7 8 9];
B = ones(3);
C = A+B; % сложение двух матриц одинакового размера
D = A+5; % сложение матрицы и числа
E = A*B; % умножение матрицы А на В
F = B*A; % умножение матрицы В на А
G = 5*A; % умножение матрицы на число
Операции вычисления обратной матрицы, а также транспонирования матриц и векторов, записываются следующим образом:
a = [1 1 1]; % вектор-строка
b = a’; % вектор-столбец, образованный
% транспонированием вектора-строки а.
A = [1 2 3; 4 5 6; 7 8 9]; % матрица 3х3 элемента
B = a*A; % B = [12 15 18] – вектор-строка
C = A*b; % C = [6; 15; 24] – вектор-столбец
D = a*A*a’; % D = 45 – число, сумма эл-ов матрицы А
E = A’; % E – транспонированная матрица А
F = inv(A); % F – обратная матрица А
G = A^-1; % G – обратная матрица А
Из приведенного примера видно, что операция транспонирования матриц и векторов обозначается символом ‘ (апостроф), который ставится после имени вектора или матрицы. Вычисление обратной матрицы можно делать путем вызова функции inv() или возводя матрицу в степень -1. Результат в обоих случаях будет одинаковым, а два способа вычисления сделано для удобства использования при реализации различных алгоритмов.
Если в процессе вычислений требуется поэлементно умножить, разделить или возвести в степень элементы вектора или матрицы, то для этого используются операторы:
.* — поэлементное умножение;
./ и . — поэлементные деления;
.^ — поэлементное возведение в степень.
Рассмотрим работу данных операторов на следующем примере.
a = [1 2 3]; % вектор-строка
b = [3 2 1]; % вектор-строка
c = a.*b; % c = [3 4 3]
A = ones(3); % матрица 3х3, состоящая из единиц
B = [1 2 3;4 5 6; 7 8 9]; % матрица 3х3
C = A.*B; % матрица 3х3, состоящая из 
D = A./B; % матрица 3х3, состоящая из 
E = A.B; % матрица 3х3, состоящая из 
F = A.^2; % возведение элементов матрицы А в квадрат
В заключении данного параграфа рассмотрим несколько функций полезных при работе с векторами и матрицами.
Для поиска максимального значения элемента вектора используется стандартная функция max(), которая возвращает найденное максимальное значение элемента и его позицию (индекс):
a = [1 6 3 4];
[v, i] = max(a); % v = 6, i = 2;
Приведенный пример показывает два разных способа вызова функции max(). В первом случае определяется и максимальное значение элемента и его индекс в векторе, а во втором – только максимальное значение элемента.
В случае с матрицами, данная функция определяет максимальные значения, стоящие в столбцах, как показано ниже в примере:
A = [4 3 5; 6 7 2; 3 1 8];
[V, I] = max(A); % V=[6 7 8], I = [2 2 3]
V = max(A); % V=[6 7 8]
Полный синтаксис функции max() можно узнать, набрав в командном окне MatLab команду
Аналогичным образом работает функция min(), которая определяет минимальное значение элемента вектора или матрицы и его индекс.
Другой полезной функцией работы с матрицами и векторами является функция sum(), которая вычисляет сумму значений элементов вектора или столбцов матрицы:
a = [3 5 4 2 1];
s = sum(a); % s = 3+5+4+2+1=15
A = [4 3 5; 6 7 2; 3 1 8];
S1 = sum(A); % S1=[13 11 15]
S2 = sum(sum(A)); % S2=39
При вычислении суммы S2 сначала вычисляется сумма значений элементов матрицы А по столбцам, а затем, по строкам. В результате, переменная S2 содержит сумму значений всех элементов матрицы А.
Для сортировки значений элементов вектора или матрицы по возрастанию или убыванию используется функция sort() следующим образом:
b1 = sort(a); % b1=[1 2 3 4 5]
b2 = sort(a, ‘descend’); % b2=[5 4 3 2 1]
b3 = sort(a, ‘ascend’); % b3=[1 2 3 4 5]
A = [4 3 5; 6 7 2; 3 1 8];
B1 = sort(A); % B1=[3 1 2
% 4 3 5
% 6 7 8]
B2 = sort(A, ‘descend’); % B2=[6 7 8
% 4 3 5
% 3 1 2]
Во многих практических задачах часто требуется найти определенный элемент в векторе или матрице. Это можно выполнить с помощью стандартной функции find(), которая в качестве аргумента принимает условие, в соответствии с которым и находятся требуемые элементы, например:
a = [3 5 4 2 1];
b1 = find(a == 2); % b1 = 4 – индекс элемента 2
b2 = find(a
= 2); % b2 = [1 2 3 5] – индексы без 2
b3 = find(a > 3); % b3 = [2 3]
В приведенном примере символ ‘==’ означает проверку на равенство, а символ ‘
=’ выполняет проверку на неравенство значений элементов вектора а. Более подробно об этих операторах будет описано в разделе условные операторы.
Еще одной полезной функцией работы с векторами и матрицами является функция mean() для вычисления среднего арифметического значения, которая работает следующим образом:
a = [3 5 4 2 1];
m = mean(a); % m = 3
A = [4 3 5; 6 7 2; 3 1 8];
M1 = mean(A); % M1 = [4.333 3.667 5.000]
M2 = mean(mean(A)); % M2 = 4.333
© 2019 Научная библиотека
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
К матричным действиям с матрицами относятся такие операции, которые используются в матричном исчислении в математике. Базовые действия с матрицами (векторами): сложение, вычитание, транспонирование, умножение матрицы на число, умножение матрицы на матрицу, возведение квадратной матрицы в степень – осуществляются в MATLAB с помощью обычных знаков арифметических операций. Условия, при которых эти операции возможны, таковы:
при сложении или вычитании матриц они должны иметь одинаковые размеры;
при умножении матриц число столбцов первого множителя должно совпадать с числом строк второго множителя.
Невыполнение этих условий приводит к появлению сообщения об ошибке.
Приведем примеры базовых действий с матрицами
>> A=[0 -2 4;3 2 1];D=[-5 4 2;1 3 1];B=[-1 -2 -3;1 3 1;0 2 2];
Пример сложения и вычитания
Пример умножения на число
Пример транспонирования матрицы, при котором ее строки становятся столбцами, а столбцы – строками, осуществляется с помощью оператора (апостроф):
В математике транспонированная матрица А обозначается А Т .
Знак закреплен за матричным умножением векторов и матриц в смысле линейной алгебры. При этом число столбцов первой матрицы обязано равняться числу строк второй матрицы. Произведение прямоугольной матрицы An×k (таблицы чисел, расположенных в n строках и в k столбцах) на матрицу Bk×m определяется следующим образом: для того, чтобы получить элемент cij матрицы — произведения C = AB, следует элементы i — й строки матрицы А умножить на соответствующие элементы j — го столбца матрицы В и результаты сложить, т. е.
Матрица С = Сn×m занимает n строк и m столбцов.
Пример умножения матрицы на матрицу
Умножение двух векторов определено в математике только для векторов одинакового размера и лишь тогда, когда один из векторов сомножителей является строкой, а второй – столбцом. Иначе говоря, если векторы Х и У являются строками, то математический смысл имеют только две формы умножения этих векторов: U = X*Y’ и V = X’*Y. Причем в первом случае результатом будет скалярное произведение векторов Х и У (число), а во втором – внешнее произведение векторов Х и Y (квадратная матрица).
Скалярное произведение двух векторов вычисляет команда dot:
Векторное произведение. Для трехкомпонентных векторов в MATLAB существует команда cross, которая вычисляет векторное произведение двух векторов.
Командаdet(B) вычисляет определитель│B│ квадратной матрицы B.
Команда обращения матрицы inv(B) вычисляет матрицу В -1 , обратную заданной матрице B. Исходная матрица B должна быть квадратной, и ее определитель не должен быть равен нулю.
-0.6667 0.3333 -1.1667
0.3333 0.3333 0.3333
-0.3333 -0.3333 0.1667
Матрица, обратная матрице В, обозначается В -1 и удовлетворяет соотношениям (В -1 ) -1 = B, ВВ -1 = В -1 В = E, где E – единичная матрица того же порядка n, что и B.
Проверим правильность выполнения операции обращения матрицы B:
-1.0000 -2.0000 -3.0000
1.0000 3.0000 1.0000
В результате получили матрицу B, т. е. соотношение (В -1 ) -1 = B выполняется.
-0.0000 1.0000 -0.0000
Соотношения ВВ -1 = В -1 В = E также выполняются.
Примеры возведения квадратной матрицы в степень
-0.6667 0.3333 -1.1667
0.3333 0.3333 0.3333
-0.3333 -0.3333 0.1667
При возведении матрицы в целую положительную степень происходит матричное умножение матрицы на саму себя столько раз, каков показатель степени. Для отрицательных степеней вычисляется степень обратной матрицы.
Если требуется извлечь квадратный корень из матрицы, то лучше применить матричную функцию sqrtm. Матричные экспонента и логарифм вычисляются при помощи матричных функций expm и logm.
В MATLABвводятся две новых операции (они не относятся к операциям линейной алгебры) деления матриц слева направо и справа налево. Первая операция записывается при помощи знака , а вторая – при помощи знака , которые помещаются между именами двух матриц – делимого и делителя. Операция B/A эквивалентна операции B*inv(A) и ее удобно использовать для решения матричного уравнения
а AB эквивалентна inv(A)*B и является решением матричного уравнения
Поэлементные действия с матрицами не являются операциями линейной алгебры, они лишь преобразуют элементы матрицы как элементы обычного двумерного массива.
Как правило, если f является одной из встроенных математических функций системы MATLAB или является заданной пользователем векторизованной функцией, то выражение f(A) представляет собой матрицу, полученную поэлементным вычислением f для A.
0.8415 0.9093 0.1411
Кроме поэлементного преобразования матриц с помощью математических функций, в MATLAB можно выполнять поэлементные преобразования матриц с помощью арифметических операций. К таким операциям относятся операции поэлементного умножения с помощью оператора (без пробела между точкой и звездочкой), поэлементного деления , обратного поэлементного деления , поэлементного возведение в степень . Операции поэлементного преобразования матриц выполняются только над матрицами одинакового размера и типа. В результате получается матрица такого же размера и типа. Проиллюстрируем поэлементные преобразования матриц на матрицах A и B:
>> A=[1 2 3 4 5;-2 3 1 4 0], B=[-1 3 5 -2 1;1 8 -3 -1 2]
Результатом поэлементного умножения матриц A и B является матрица, каждый элемент которой представляет собой произведение соответствующих элементов матриц A и B.
-1.0000 0.6667 0.6000 -2.0000 5.0000
-2.0000 0.3750 -0.3333 -4.0000 0
Результат – матрица, элементы которой являются частным от деления соответствующих элементов матриц A и B.
Обратное поэлементное деление
Warning: Divide by zero.
-1.0000 1.5000 1.6667 -0.5000 0.2000
-0.5000 2.6667 -3.0000 -0.2500 Inf
Результатом является матрица, элементы которой являются частным от деления соответствующих элементов матриц B и A.
Поэлементное возведение в степень
0.0010 0.0080 0.2430 0.0001 0.0050
-0.0020 6.5610 0.0010 0.0003 0
При поэлементном возведении в степень каждый элемент матрицы A возводится в степень, равную соответствующему элементу матрицы B.
Обратим внимание на результат, полученный при выполнении операции A.^B. Система MATLAB выделила общий множитель 1.0e+003 * для всех элементов результирующей матрицы.
Оригинальной в MATLAB является операция прибавления к матрице числа. Она записывается таким образом: A+x или x+A (где A – матрица, а x – число). Такая операция также не относится к операциям линейной алгебры. Например:
При поэлементном возведении в степень показателем степени может быть не только матрица того же размера, что и исходная, но и число:
В MATLAB поэлементные операции над векторами аналогичны поэлементным операциям над матрицами.
Таким образом, система MATLAB является совершенным инструментом для работы с массивами. MATLAB позволяет выполнять мощные групповые вычисления над массивами, используя обычные математические операторы и функции. В традиционных языках программирования математические действия производятся только над скалярами. Матричные команды MATLAB чрезвычайно компактны по записи, но выполняют гигантский объем работы. Более того, матричные вычисления в MATLAB выполняются значительно быстрее, чем скалярные.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9517 —  | 7342 —
| 7342 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
С упорядоченной последовательностью действительных чисел a1,a2, … , an можно связать понятие связанного вектора в n-мерном пространстве и обозначить как:

Типы и характеристики векторов.
Нулевой вектор – вектор, все компоненты которого равны нулю.
Единичный вектор – вектор, длина которого равна единице:
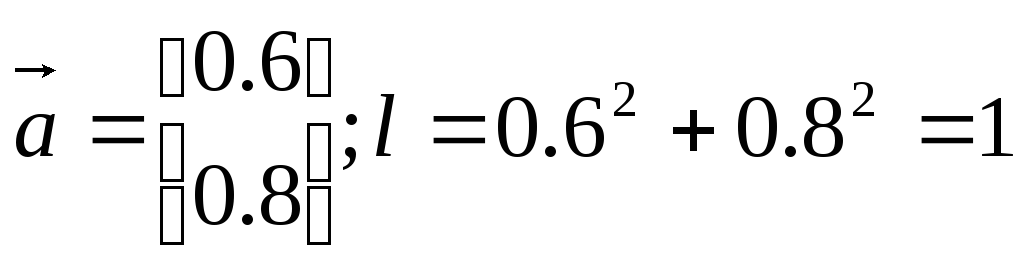
Транспонированный вектор – вектор, компоненты которого располагаются в виде строки:
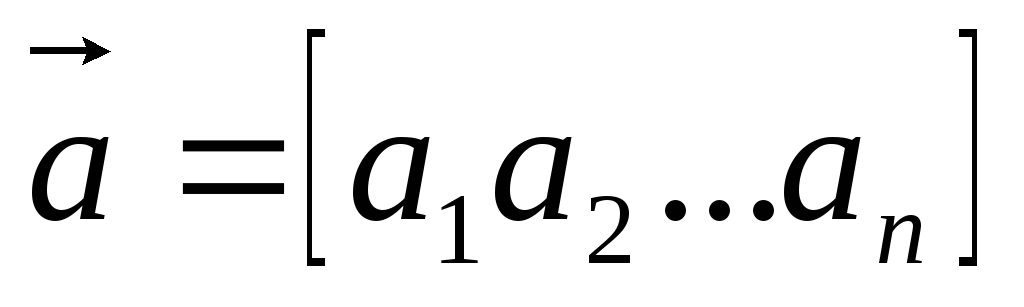
Два вектора с одинаковой размерностью равны тогда, когда равны их соответствующие компоненты:

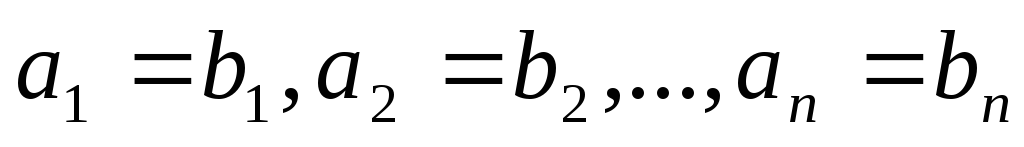 , где i = 1, 2, 3, …, n
, где i = 1, 2, 3, …, n
Совокупность чисел расположенных в прямоугольной таблице, состоящей из n строк и m столбцов, называется матрицей и обозначается как:

Положение элемента  в матрице определяется двумя индексами (i и j), где i – номер строки
в матрице определяется двумя индексами (i и j), где i – номер строки  , а j – номер столбца
, а j – номер столбца 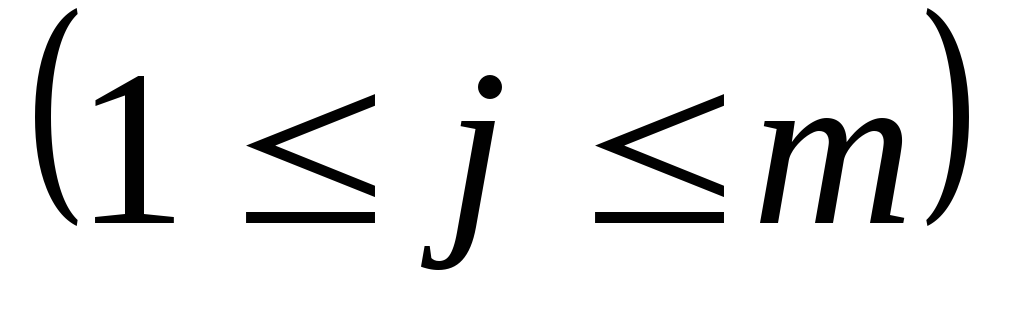
Вектор строка – матрица, состоящая из одной строки n=1
Вектор столбец – матрица, состоящая из одного столбца m=1
Квадратная матрица – матрица, у которой n = m
Верхне треугольная – матрица, у которой  при i>j
при i>j


