Сложение векторов по буквам

Как происходит сложение векторов, не всегда понятно ученикам. Дети не представляют того, что за ними скрывается. Приходится просто запоминать правила, а не вдумываться в суть. Поэтому именно о принципах сложения и вычитания векторных величин требуется много знаний.

В результате сложения двух и более векторов всегда получается еще один. Причем он всегда обязательно будет одинаковым, независимо от приема его нахождения.

Чаще всего в школьном курсе геометрии рассматривается сложение двух векторов. Оно может быть выполнено по правилу треугольника или параллелограмма. Эти рисунки выглядят по-разному, но результат от действия один.

Как происходит сложение по правилу треугольника?

Оно применяется тогда, когда векторы неколлинеарные. То есть не лежат на одной прямой или на параллельных.

В этом случае от некоторой произвольной точки нужно отложить первый вектор. Из его конца требуется провести параллельный и равный второму. Результатом станет вектор, исходящий из начала первого и завершающийся в конце второго. Рисунок напоминает треугольник. Отсюда и название правила.

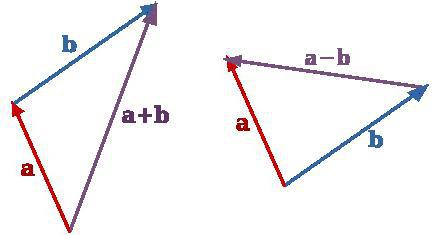
Если векторы коллинеарные, то это правило тоже можно применять. Только рисунок будет расположен вдоль одной линии.

Как выполняется сложение по правилу параллелограмма?

Опять же? применяется только для неколлинеарных векторов. Построение выполняется по другому принципу. Хотя начало такое же. Нужно отложить первый вектор. И от его начала — второй. На их основе достроить параллелограмм и провести диагональ из начала обоих векторов. Она и будет результатом. Так выполняется сложение векторов по правилу параллелограмма.

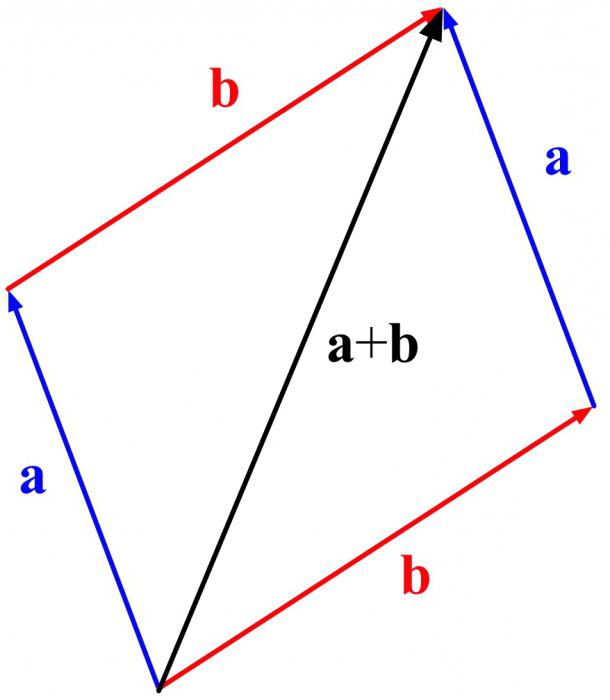
До сих пор их было два. А как быть, если их 3 или 10? Использовать следующий прием.

Как и когда применяется правило многоугольника?

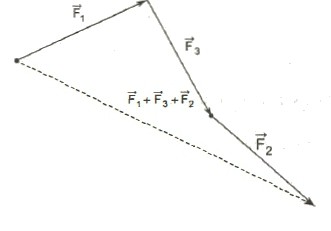
Если требуется выполнить сложение векторов, число которых — больше двух, пугаться не стоит. Достаточно последовательно отложить их все и соединить начало цепочки с ее концом. Этот вектор и будет искомой суммой.

Какие свойства действительны для действий с векторами?

О нулевом векторе. Которое утверждает, что при сложении с ним получается исходный.

О противоположном векторе. То есть о таком, который имеет противоположное направление и равное по модулю значение. Их сумма будет равна нулю.

О коммутативности сложения. То, что известно еще с начальной школы. Смена мест слагаемых не приводит к изменению результата. Другими словами, неважно какой вектор откладывать сначала. Ответ все равно будет верным и единственным.

Об ассоциативности сложения. Этот закон позволяет складывать попарно любые векторы из тройки и к ним прибавлять третий. Если записать это с помощью знаков, то получится следующее:

первый + (второй + третий) = второй + (первый + третий) = третий + (первый + второй).

Что известно о разности векторов?

Отдельной операции вычитания не существует. Это связано с тем, что оно, по сути, является сложением. Только второму из них задается противоположное направление. А потом все выполняется так, как если бы рассматривалось сложение векторов. Поэтому об их разности практически не говорят.

Для того чтобы упростить работу с их вычитанием, видоизменено правило треугольника. Теперь (при вычитании) второй вектор нужно отложить из начала первого. Ответом будет тот, что соединяет конечную точку уменьшаемого с ней же вычитаемого. Хотя можно и откладывать так, как было описано ранее, просто изменив направление второго.

Как найти сумму и разность векторов в координатах?

В задаче даны координаты векторов и требуется узнать их значения для итогового. При этом построений выполнять не нужно. То есть можно воспользоваться несложными формулами, которые описывают правило сложения векторов. Они выглядят так:

а (х, у, z) + в (k, l, m) = с (х+k, y+l, z+m);

а (х, у, z) -в (k, l, m) = с (х-k, y-l, z-m).

Легко заметить, что координаты нужно просто сложить или вычесть в зависимости от конкретного задания.

Первый пример с решением

Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.

Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.

Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.

А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.

Ответ. Разность АО и ВО равна 8 см.

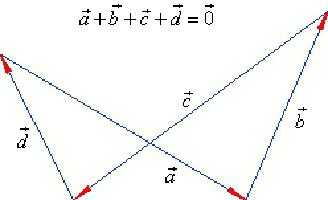
Второй пример и его подробное решение

Условие. У ромба АВСД диагонали равны 12 и 16 см. Точка их пересечения обозначена буквой О. Вычислите длину вектора, образованного разностью векторов АО и ВО.

Решение. Пусть обозначение вершин ромба будет таким же, как в предыдущей задаче. Аналогично решению первого примера получается, что искомая разность равна вектору АВ. А его длина неизвестна. Решение задачи свелось к тому, чтобы вычислить одну из сторон ромба.

Для этой цели потребуется рассмотреть треугольник АВО. Он прямоугольный, потому что диагонали ромба пересекаются под углом в 90 градусов. А его катеты равны половинам диагоналей. То есть 6 и 8 см. Искомая в задаче сторона совпадает с гипотенузой в этом треугольнике.

Для ее нахождения потребуется теорема Пифагора. Квадрат гипотенузы будет равен сумме чисел 6 2 и 8 2 . После возведения в квадрат получатся значения: 36 и 64. Их сумма — 100. Отсюда следует, что гипотенуза равна 10 см.

Ответ. Разность векторов АО и ВО составляет 10 см.

Третий пример с детальным решением

Условие. Вычислить разность и сумму двух векторов. Известны их координаты: у первого — 1 и 2, у второго — 4 и 8.

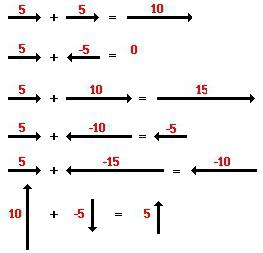
Решение. Для нахождения суммы потребуется сложить попарно первые и вторые координаты. Результатом будут числа 5 и 10. Ответом будет вектор с координатами (5; 10).

Для разности нужно выполнить вычитание координат. После выполнения этого действия получатся числа -3 и -6. Они и будут координатами искомого вектора.

Ответ. Сумма векторов — (5; 10), их разность — (-3; -6).

Четвертый пример

Условие. Длина вектора АВ равна 6 см, ВС — 8 см. Второй отложен от конца первого под углом в 90 градусов. Вычислить: а) разность модулей векторов ВА и ВС и модуль разности ВА и ВС; б) сумму этих же модулей и модуль суммы.

Решение: а) Длины векторов уже даны в задаче. Поэтому вычислить их разность не составит труда. 6 — 8 = -2. Несколько сложнее обстоит дело с модулем разности. Сначала нужно узнать, какой вектор будет являться результатом вычитания. Для этой цели следует отложить вектор ВА, который направлен в противоположную сторону АВ. Потом от его конца провести вектор ВС, направив его в сторону, противоположную исходному. Результатом вычитания получится вектор СА. Его модуль можно вычислить по теореме Пифагора. Несложные вычисления приводят к значению 10 см.

б) Сумма модулей векторов получается равной 14 см. Для поиска второго ответа потребуется некоторое преобразование. Вектор ВА противоположно направлен тому, который дан — АВ. Оба вектора направлены из одной точки. В этой ситуации можно использовать правило параллелограмма. Результатом сложения будет диагональ, причем не просто параллелограмма, а прямоугольника. Его диагонали равны, значит, модуль суммы такой же, как в предыдущем пункте.

Что такое вектор?

Вектор это образок с направлением.

Вектор и луч часто путают и допускают грубую ошибку. Вектор то направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой. Луч имеет начало и направление, но он бесконечен, то есть измерить его невозможно. Так же, как нельзя и складывать лучи между собой или луч с вектором.

Вектор иногда помещают в декартову систему координат. Тогда проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси х и у. Каждая из этих проекций будет отрезком. При этом, если из проекций составить прямоугольник, то его гипотенуза и будет начальным вектором. Это иногда используется при сложении векторов.

Рис. 1. Вектор в системе координат.

Сложение и вычитание векторов

Способов и методов сложения векторов всего два. Существует и третий, но его не считают отдельным методом, так как он проистекает из первых двух. Но мы его рассмотрим отдельно, чтобы не возникало вопросов при дальнейшем изучении темы.

Правило многоугольника

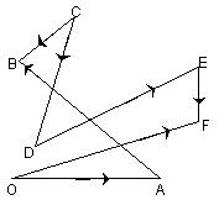
Для того, чтобы сложить вектора правилом многоугольника, необходимо параллельным переносом совместить конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не кончатся вектора, которые необходимо складывать.

После этого нужно конец последнего вектора соединить с началом первого и указать направление. Получившийся вектор будет направлен в сторону последнего из учавствовавших в сложении.

Складывать таким способом можно любое количество векторов. Если так складывается только два вектора, то способ называют правилом треугольника

Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер. Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.

Рис. 2. Правило многоугольника.

Правило параллелограмма

Правило параллелограмма сложнее, его можно применять только для 2 векторов. Если вам нужно этим способом сложить большее количество векторов, например, три, то действие выполняют в следующем порядке:

• Складывают два любых вектора правилом параллелограмма. Результатом будет некий вектор и у нас остается еще один, который в сложении не участвовал.
• Получившийся и оставшийся вектора складывают по тому же правилу.
• Этот процесс можно повторять столько раз, сколько требуется по условию задачи.

Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого получившуюся фигуру достраивают до параллелограмма. Диагональ, которая выходит из начала двух векторов и есть результат сложения. Вектор должен быть направлен в противоположную сторону от совмещенного начала двух векторов.

Для того чтобы вычесть вектора любым способом, направление вектора, который является вычитаемым, меняют на противоположное. Получившиеся вектора складывают любым из методов.

Рис. 3. Правило прямоугольника.

Сложение в декартовой системе

В декартовой системе все вектора раскладывают на проекции, после чего отрезки проекций складывают: проекции на ось х отдельно, на ось у отдельно. После из получившихся двух проекций снова собирают вектор.

Что мы узнали?

Мы узнали, что такое вектор. Поговорили о правилах сложении и вычитании векторов. Обсудили, чем отличается вектор от луча и обсудили метод действий с векторами в декартовой системе координат.

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + >
ight) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec <0>)

Длина нулевого вектора равна нулю:
( left| vec <0>
ight| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <— , — , — >
ight) )

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrow
ight|=left|k
ight||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .