Содержание
Обход в глубину (поиск в глубину, англ. Depth-First Search, DFS) — один из основных методов обхода графа, часто используемый для проверки связности, поиска цикла и компонент сильной связности и для топологической сортировки.
Содержание
Алгоритм [ править ]
Общая идея [ править ]
Общая идея алгоритма состоит в следующем: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.
Пошаговое представление [ править ]
- Выбираем любую вершину из еще не пройденных, обозначим ее как [math]u[/math] .
- Запускаем процедуру [math]mathrm[/math]
- Помечаем вершину [math]u[/math] как пройденную
- Для каждой не пройденной смежной с [math]u[/math] вершиной (назовем ее [math]v[/math] ) запускаем [math]mathrm[/math]
- Повторяем шаги 1 и 2, пока все вершины не окажутся пройденными.
Реализация [ править ]
В массиве [math]mathrm[/math] хранится информация о пройденных и не пройденных вершинах.
Время работы [ править ]
Оценим время работы обхода в глубину. Процедура [math]mathrm
Цвета вершин [ править ]
Зачастую, простой информации "были/не были в вершине" не хватает для конкретных целей.
Поэтому в процессе алгоритма вершинам задают некоторые цвета:
- если вершина белая, значит, мы в ней еще не были, вершина не пройдена;
- серая — вершина проходится в текущей процедуре [math]mathrm
[/math] ; - черная — вершина пройдена, все итерации [math]mathrm
[/math] от нее завершены.
Такие "метки" в основном используются при поиске цикла.
Реализация [ править ]
Отличие реализации с цветами от предыдущей лишь в массиве [math]mathrm[/math] , который мы назовем теперь [math]mathrm[/math] . В нем будет хранится информация о цветах вершин.
Пример [ править ]
Рассмотрим, как будут изменяться цвета вершин при обходе в глубину данного графа.
| Описание шага | Состояние графа |
|---|---|
| В функции [math]mathrm |
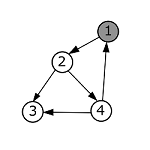 |
| Пробуем пойти в вершину с номером 2. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет. | 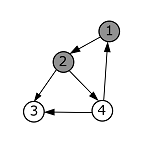 |
| Пробуем пойти в вершину с номером 3. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет. | 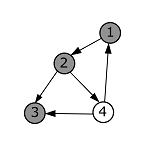 |
| Проверяем, что из вершины с номером 3 не исходит ни одного ребра. Помечаем ее в черный цвет и возвращаемся в вершину с номером 2. | 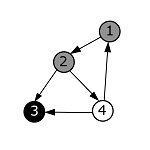 |
| Пробуем пойти в вершину с номером 4. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет. | 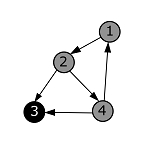 |
| Пробуем пойти в вершину с номером 3. Видим, что она черного цвета, и остаемся на месте. |  |
| Пробуем пойти в вершину с номером 1. Видим, что она серого цвета, и остаемся на месте. |  |
| Из вершины с номером 4 больше нет исходящих ребер. Помечаем ее в черный цвет и возвращаемся в вершину с номером 2. | 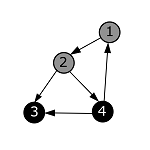 |
| Из вершины с номером 2 больше нет исходящих ребер. Помечаем ее в черный цвет и возвращаемся в вершину с номером 1. | 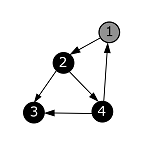 |
| Из вершины с номером 1 больше нет исходящих ребер. Помечаем ее в черный цвет и выходим в программу [math]mathrm |
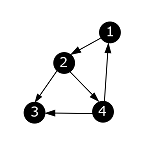 |
Дерево обхода в глубину [ править ]
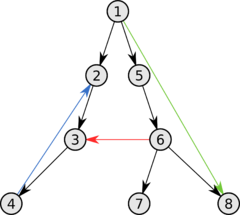
Рассмотрим подграф предшествования обхода в глубину [math]G_p = (V, E_p)[/math] , где [math]E_p = <(p[u], u) : u in V, p[u]
eq NIL>[/math] , где в свою очередь [math]p[u][/math] — вершина, от которой был вызван [math]mathrm [/math] (для вершин, от которых [math]mathrm
- Ребрами дерева назовем те ребра из [math]G[/math] , которые вошли в [math]G_p[/math] .
- Ребра [math](u, v)[/math] , соединяющие вершину [math]u[/math] с её предком [math]v[/math] в дереве обхода в глубину назовем обратными ребрами (для неориентированного графа предок должен быть не родителем, так как иначе ребро будет являться ребром дерева).
- Ребра [math](u, v)[/math] , не являющиеся ребрами дерева и соединяющие вершину [math]u[/math] с её потомком [math]v[/math] в дереве обхода в глубину назовем прямыми ребрами (в неориентированном графе нет разницы между прямыми и обратными ребрами, поэтому все такие ребра считаются обратными).
- Все остальные ребра назовем перекрестными ребрами — такие ребра могут соединять вершины одного и того же дерева обхода в глубину, когда ни одна из вершин не является предком другой, или соединять вершины в разных деревьях.
Алгоритм [math]mathrm
- Белый цвет вершины [math]v[/math] по определению [math]mathrm
[/math] говорит о том, что это ребро дерева. - Серый цвет в силу того, что серые вершины всегда образуют нисходящий путь в каком-либо из деревьев [math]mathrm
[/math] и встреченная вершина [math]v[/math] лежит на нем выше вершины [math]u[/math] , определяет обратное ребро (для неориентированного графа необходимо проверить условие [math]v
eq p[u][/math] ). - Черный цвет, соответственно, указывает на прямое или перекрестное ребро.
Поиск в глубину
При поиске в глубину посещается первая вершина , затем необходимо идти вдоль ребер графа, до попадания в тупик . Вершина графа является тупиком, если все смежные с ней вершины уже посещены. После попадания в тупик нужно возвращаться назад вдоль пройденного пути, пока не будет обнаружена вершина , у которой есть еще не посещенная вершина , а затем необходимо двигаться в этом новом направлении. Процесс оказывается завершенным при возвращении в начальную вершину, причем все смежные с ней вершины уже должны быть посещены.
Таким образом, основная идея поиска в глубину – когда возможные пути по ребрам , выходящим из вершин, разветвляются, нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).
Алгоритм поиска в глубину
Шаг 1. Всем вершинам графа присваивается значение не посещенная. Выбирается первая вершина и помечается как посещенная.
Шаг 2. Для последней помеченной как посещенная вершины выбирается смежная вершина , являющаяся первой помеченной как не посещенная, и ей присваивается значение посещенная. Если таких вершин нет, то берется предыдущая помеченная вершина .
Шаг 3. Повторить шаг 2 до тех пор, пока все вершины не будут помечены как посещенные ( рис. 44.5).

Также часто используется нерекурсивный алгоритм поиска в глубину. В этом случае рекурсия заменяется на стек . Как только вершина просмотрена, она помещается в стек , а использованной она становится, когда больше нет новых вершин, смежных с ней.
Временная сложность зависит от представления графа. Если применена матрица смежности , то временная сложность равна O(n 2 ) , а если нематричное представление – O(n+m) : рассматриваются все вершины и все ребра .
Поиск в ширину
При поиске в ширину , после посещения первой вершины, посещаются все соседние с ней вершины. Потом посещаются все вершины, находящиеся на расстоянии двух ребер от начальной. При каждом новом шаге посещаются вершины, расстояние от которых до начальной на единицу больше предыдущего. Чтобы предотвратить повторное посещение вершин, необходимо вести список посещенных вершин. Для хранения временных данных, необходимых для работы алгоритма, используется очередь – упорядоченная последовательность элементов, в которой новые элементы добавляются в конец, а старые удаляются из начала.
Таким образом, основная идея поиска в ширину заключается в том, что сначала исследуются все вершины, смежные с начальной вершиной ( вершина с которой начинается обход). Эти вершины находятся на расстоянии 1 от начальной. Затем исследуются все вершины на расстоянии 2 от начальной, затем все на расстоянии 3 и т.д. Обратим внимание, что при этом для каждой вершины сразу находятся длина кратчайшего маршрута от начальной вершины.
Алгоритм поиска в ширину
Шаг 1. Всем вершинам графа присваивается значение не посещенная. Выбирается первая вершина и помечается как посещенная (и заносится в очередь ).
Шаг 2. Посещается первая вершина из очереди (если она не помечена как посещенная). Все ее соседние вершины заносятся в очередь . После этого она удаляется из очереди.
Шаг 3. Повторяется шаг 2 до тех пор, пока очередь не пуста ( рис. 44.6).
Сложность поиска в ширину при нематричном представлении графа равна O(n+m) , ибо рассматриваются все n вершин и m ребер. Использование матрицы смежности приводит к оценке O(n 2 )
Ключевые термины
Вес (длина) ребра – это число или несколько чисел, которые интерпретируются по отношению к ребру как длина , пропускная способность .
Вес вершины – это число (действительное, целое или рациональное), поставленное в соответствие данной вершине.
Взвешенный граф – это граф , каждому ребру которого поставлен в соответствие его вес .
Граф – это совокупность двух конечных множеств: множества точек и множества линий, попарно соединяющих некоторые из этих точек.
Вершины (узлы) графа – это множество точек, составляющих граф .
Замкнутый маршрут – это маршрут в графе, у которого начальная и конечная вершины совпадают.
Кратные ребра – это ребра , соединяющие одну и ту же пару вершин.
Маршрут в графе – это конечная чередующаяся последовательность смежных вершин и ребер, соединяющих эти вершины.
Матрица инцидентности – это двумерный массив , в котором указываются связи между инцидентными элементами графа ( ребро и вершина ).
Матрица смежности – это двумерный массив , значения элементов которого характеризуются смежностью вершин графа
Мультиграф – это граф , у которого любые две вершины соединены более чем одним ребром .
Неориентированный граф (неорграф) – это граф , у которого все ребра неориентированы, то есть ребрам которого не задано направление.
Обход графа (поиск на графе) – это процесс систематического просмотра всех ребер или вершин графа с целью отыскания ребер или вершин, удовлетворяющих некоторому условию.
Ориентированный граф (орграф) – это граф , у которого все ребра ориентированы, то есть ребрам которого присвоено направление.
Открытый маршрут – это маршрут в графе, у которого начальная и конечная вершины различны.
Петля – это ребро , соединяющее вершину саму с собой.
Поиск в глубину – это обход графа по возможным путям, когда нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).
Поиск в ширину – это обход графа по возможным путям, когда после посещения вершины, посещаются все соседние с ней вершины.
Простой граф – это граф , в котором нет ни петель, ни кратных ребер.
Путь – это открытая цепь, у которой все вершины различны.
Ребра (дуги) графа – это множество линий, соединяющих вершины графа .
Связный граф – это граф , у которого для любой пары вершин существует соединяющий их путь .
Смежные вершины – это вершины, соединенные общим ребром .
Смешанный граф – это граф , содержащий как ориентированные, так и неориентированные ребра .
Список ребер – это множество, образованное парами смежных вершин
Тупик – это вершина графа, для которой все смежные с ней вершины уже посещены
Цепь – это маршрут в графе, у которого все ребра различны.
Цикл – это замкнутая цепь, у которой различны все ее вершины, за исключением концевых.
Это один из основных алгоритмов на графах.
В результате поиска в глубину находится лексикографически первый путь в графе.
Алгоритм работает за O (N+M).
Применения алгоритма
- Поиск любого пути в графе.
- Поиск лексикографически первого пути в графе.
- Проверка, является ли одна вершина дерева предком другой:
В начале и конце итерации поиска в глубину будет запоминать "время" захода и выхода в каждой вершине. Теперь за O(1) можно найти ответ: вершина i является предком вершины j тогда и только тогда, когда starti endj. - Задача LCA (наименьший общий предок).
- Топологическая сортировка:
Запускаем серию поисков в глубину, чтобы обойти все вершины графа. Отсортируем вершины по времени выхода по убыванию — это и будет ответом. - Проверка графа на ацикличность и нахождение цикла
- Поиск компонент сильной связности:
Сначала делаем топологическую сортировку, потом транспонируем граф и проводим снова серию поисков в глубину в порядке, определяемом топологической сортировкой. Каждое дерево поиска — сильносвязная компонента. - Поиск мостов:
Сначала превращаем граф в ориентированный, делая серию поисков в глубину, и ориентируя каждое ребро так, как мы пытались по нему пройти. Затем находим сильносвязные компоненты. Мостами являются те рёбра, концы которых принадлежат разным сильносвязным компонентам.
Реализация
Это наиболее общий код. Во многих случаях времена захода и выхода из вершины не важны, так же как и не важны цвета вершин (но тогда надо будет ввести аналогичный по смыслу булевский массив used). Вот наиболее простая реализация:


