Свойства единицы в математике

Математика – это совокупность наук, изучающих величины, количественные отношения, а также пространственные формы. Изучение математики начинается с раздела арифметики.

Арифметика – это наука о числах. В арифметике изучаются простейшие свойства чисел и различные способы вычислительных операций над ними.

Основополагающими понятиями в арифметике являются счёт, единица и число.

Определение счёта, единицы и числа

Чтобы узнать количество объектов (например, карандашей) или действий (например, приседаний), их нужно сосчитать. Счёт – это определение количества чего-либо.

Каждый отдельный объект или каждое отдельное действие при счёте называется единицей. Результат счёта, то есть количество посчитанных единиц, выражается числом. Число – это определённое (посчитанное) количество единиц.

Число позволяет дать ответ на вопрос сколько? (например: сколько яблок на тарелке?).

Числа можно выражать двумя способами: устно и письменно, с помощью специальных символов. Способ выражать числа устно называется устной нумерацией. Способ выражать числа письменными знаками (символами) называется письменной нумерацией.

Множества

В математике любую группу объектов можно назвать множеством. Каждый объект из группы называется элементом множества.

На картинке изображено два множества: множество цифр и множество геометрических фигур. Цифра 5 – элемент множества цифр, а квадрат — элемент множества геометрических фигур.

Множество – это группа объектов, объединённых по какому-то общему признаку.

Если множества состоят из одних и тех же объектов, то они равны, а если из разных объектов, то не равны:

Разделы: Математика

Класс: 5

Учебник-собеседник 5 кл. авт. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В.

Цель урока: познакомить учащихся со свойствами числа 1.

Обучающие:

• Обобщить знания учащихся о свойствах единицы.
• Получить свойство: "Степень числа 1"
• Выяснить вопрос: "Чему равно частное 1:а?"

Воспитательные: Воспитывать интерес к урокам математики через межпредметные связи с литературой.

Слово учителя: "Обратите внимание на слова древнегреческого драматурга Эсхила, взятые в качестве эпиграфа урока:

"Послушайте, что смертным сделал я — число им изобрел".

Сегодня на уроке вспомним все изученные свойства единицы, еще узнаем что-то новое про единицу, увидим, какое большое значение имеет единица в математике.

"Твой ум без числа ничего не постигает". И вы докажете это на уроке.

1. Работа по учебнику-собеседнику.

2. Обсуждение вопросов.

3. Устная работа

4. Введение свойства степени 1.

5. Работа в тетради.

6. Рефлексия урока.

Работаем по учебнику-собеседнику. Разбираем самостоятельно урок 21. Читаем до первого звоночка. Ваша задача: познакомиться с вопросами, ответить на них. Обсуждаем прочитанное, затем вы читаете далее.

Итак, стр.75, урок 21. Вопросы 1-2.

Обсуждение вопросов:

1. Чем знаменательно число единица в натуральном ряду?

Ответ: С него начинается натуральный ряд.

2. Какие числа называем натуральными?

Ответ: Числа, которыми пользуемся для пересчета предметов.

3. Каким свойством обладает число 1 при сложении? При вычитании?

Ответ: Если к натуральному числу прибавить единицу, то получится следующее натуральное число: n+1.Применяя многократно действие сложения числа 1, можно получить любое натуральное число. Натуральный ряд бесконечен. Если из натурального числа вычесть 1, то получится предыдущее число.

Существует ли самое маленькое число? А самое большое натуральное число? Назовите последующее и предыдущее числа 5178.

Далее читаете до второго звоночка материал параграфа.

1. Каким свойством обладает число 1 при умножении?

Ответ: Если один из множителей равен 1, то произведение равно другому множителю.

Что получится, если данное число разделить на 1?

А если данное число разделить на себя?

Поработаем устно.

• 1+1 * 1-1:1+(1+1-1):1-1(1+1)
• 3208:3208 * 5628:5628
• 317 * 1+233:1
• (657-656) * 49-36
• 4506 * 0+6473:1
• 7218:7218+999 * 1
• 634:(1000-999)+66

Все ли действия мы с вами вспомнили? Существует ещё одно свойство единицы. Послушайте мою сказку и сформулируйте его.

Много лет прослужила Единица без единого замечания, и нужно же было как-то отметить её заслуги! Поэтому 1 решили возвести в степень. Сначала возвели во вторую степень. Думали этим и ограничиться, но опять Единица служит прилежно, а замечаний хоть бы одно! Возвели 1 в третью степень. И опять ни одного замечания. Возвели в четвертую, ни одного замечания! Подумать только! Возвели в 5-ю, в 6-ю, в 10-ю, в 100-ю. Нет замечаний! Далеко пошла Единица. Теперь она Единица в 1000-ой степени. А что изменилось от этого? Ничего — ровным счетом. Ведь Единица в 1000=ой степени — та же Единица. И на 1000-ю долю не больше!

1. А теперь сформулируйте ещё одно свойство единицы.

Ответ: возведение в степень.

2. Что получим, если 1 возведем в любую степень?

Ответ: единица. Докажите.

3. А если любое число возвести в 1 степень?

Ответ: данное число. Докажите.

4. Вычислите устно (1 2000 + 199 1 ) * 10

Работаем в тетради.

1) Пользуясь тремя пятерками и какими угодно знаками математических действий, напишите выражение равное 1.

2) Между некоторыми цифрами 12345 поставьте знаки действия и скобки так, чтобы получилась 1.

3) Из четырех двоек и любых знаков действия и скобок напишите выражение, равное 1.

Итог урока. Число 1 в математике играет, как мы убедились, большую роль. Мы с вами разобрали его свойства при действиях сложения, вычитания, умножения, деления, возведения в степень, но не ответили на вопрос: Чему равно частное 1:а?

Домашнее задание: Урок №21, №218(в; г), сочинить математическую сказку, героем которой может быть любое число или действие с числами. Попытайтесь найти ответ на вопрос: "Чему равно частное 1:а?", пользуясь математическими справочниками.

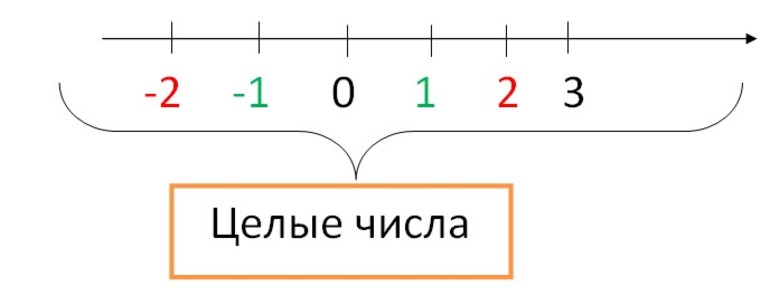
Исторические данные

Математика зародилась одновременно с необходимостью подсчета. Группа натуральных чисел появилась еще во времена первобытных людей. Они считали количество овец, дней, людей. Позже человек познакомился со сложением и вычитанием. Умножение и деление появились позже, их считали пакетными суммой и разностью (к примеру, 2х3 = 2+2+2).

Ноль первыми начали применять индийские математики. Сначала он использовался как цифра для позиционной записи чисел, постепенно он превратился в полноценную. В Древнем Китае и Индии возникла отрицательная группа, хотя Вавилон, Греция и Египет были не согласны с ее существованим. Если в результате расчетов получалось значение со знаком минус, его отвергали как невозможное. Но Диофант в третьем веке уже умел умножать отрицательные цифры. А через четыре столетия их важность признали и другие математики.

В Европе отрицательные числа считались мнимыми, ложными или абсурдными. И только после выхода работы Пизанского «Книга абака» в 1202 их начали использовать для записи долгов. В XVII веке появилась аналитическая геометрия, цифры со знаком минус нашли свое место на координатной оси. Но еще долгое время оставались непонятными арифметические действия с ними. А в XIX столетии Гамильтон и Грассман создали полную теорию отрицательных чисел.

Свойства чисел

В математике существуют три основных арифметических действия: умножение, сложение и вычитание. И для каждой операции множеству целых чисел присущи некоторые свойства:

• вычитание и сложение — коммутативность, ассоциативность, противоположного элемента и нуля;
• возведение в степень и умножение — добавляется дистрибутивность и свойство единицы;
• упорядоченность;
• делимость.

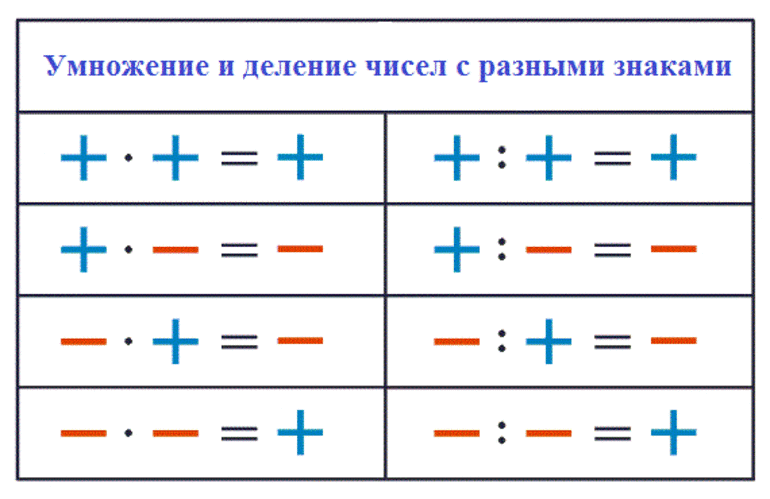
В первом случае используется правило знаков при открытии скобок: -(-а) = а, -(а+в) = -а-в, -(а-в) = -а+в. Если складываются только положительные или отрицательные значения, то суммируются их величины. А если знаки разные, то из большего вычитают меньшее и приписывают символ уменьшаемого. С целыми выражениями вычитание выполнимо всегда. Некоторым сложно считать выражения с разными знаками. Тогда можно представить себе цифры на координатной оси. При сложении положительных нужно двигаться вправо, отрицательных — влево. В случае вычитания все наоборот.

Произведение чисел с разными знаками отрицательно, в остальных случаях оно положительно: (-а)в = а (-в) = -ав и (-а)(-в) = ав. Целые цифры возводятся в степень так же, как и натуральные. Если это произведение, то нужно возвести каждый множитель, в выражениях с одинаковым основанием показатели складываются, при делении они вычитаются.

Упорядоченность необходима для сравнения целых чисел. Положительными являются те, что больше нуля, отрицательными — меньше. При сравнении выражений с минусовыми знаками большим оказывается то, у которого меньше абсолютная величина.

Делиться целый ряд может с остатком или нацело. В первом случае формула будет содержать делимое, делитель, неполное частное и всегда положительный остаток. Если это деление нацело, то остаток равен нулю. У каждого целого выражения n, которое не равно 0 или 1, есть четыре тривиальных делителя: n и — n, 1 и -1. Если других нет, то это выражение называется простым.

В алгебре для натуральных чисел есть возможность разложить их на простые множители. Это же определение присуще и целой группе, но нужно учитывать знаки.

Основные виды

Есть несколько видов целых выражений, которыми можно оперировать при расчетах. Основные из них:

• вещественные;
• неположительные;
• неотрицательные.

В некоторых задачах ответ нужно округлить до целого значения, то есть заменить его более подходящим выражением из этого ряда. Если оно изменяется в меньшую сторону, то обозначается по правилу Гаусса или Лежандра: [ x ] или E (x). А когда нужно округлить до большего значения, то применяется функция «потолок». Также можно убрать дробную часть или записать ближайшее целое число.

Вещественный ряд в любом случае можно приблизить рациональным, это связывает его с целыми выражениями.

Лучшим инструментом для выполнения этой задачи считаются цепные или непрерывные дроби. К примеру, необходимо разложить число Пи: десятичную дробь 3,14159265 записывают в виде обыкновенных и целого числа — 3, 22/7, 333/106, 355/113. Наиболее подходящим является второе выражение — 22/7.

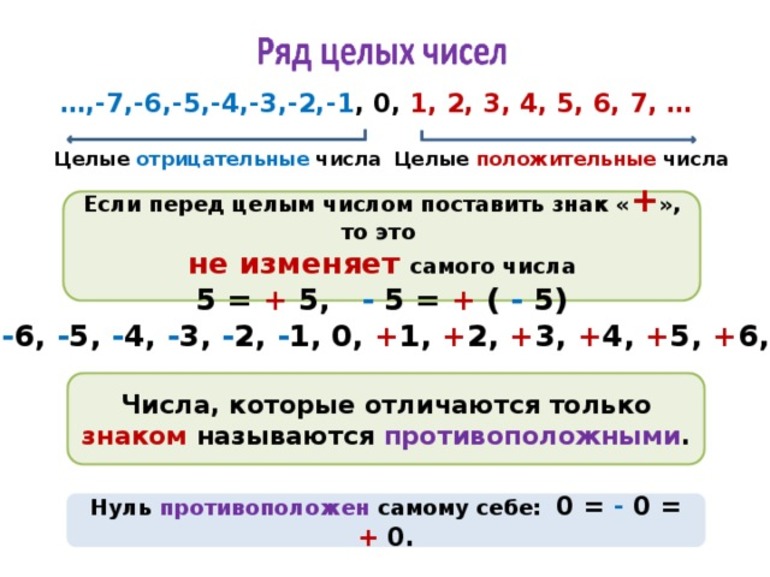
Целые выражения бывают неположительными и неотрицательными. К первым относят все со знаком минус и нуль, ко вторым — со знаком плюс. А сам 0 нельзя назвать ни положительным, ни отрицательным. Используется такое высказывание для упрощения. Можно не говорить, что а больше или равно нулю, достаточно сказать: оно неотрицательное. Простые примеры целых чисел для двух случаев: 0, 13, 28 и 0, -7, -24.

Описание изменения величин

Класс целых значений применяется для описания изменения различных величин. В частности, с их помощью решают простые задачи: на складе хранится 400 насосов, 300 привезли вчера, а 200 увезли сегодня, нужно найти остаток. Если добавилось 300 предметов, то их записывают со знаком плюс: 400+300 = 700. А для уменьшения количества перед числом ставят минус: 700−200 = 500. Искомое выражение — 500 насосов. Если никаких передвижений товаров не будет, то на неизменность количества укажет нуль.

Основное преимущество целых значений перед натуральными заключается в том, что они четко характеризуют увеличение или уменьшение величин. Удобно использовать их при описании температуры воздуха. Мороз записывают именно отрицательными числами, а тепло — положительными.

А также они применяются в финансовых расчетах. Если человек должен отдать кому-то 10 долларов, то на данный момент у него есть -10 долл. То есть долги можно записать отрицательными числами, а прибыль — положительными. Общую задолженность также узнают с помощью целого ряда: если за электроэнергию нужно заплатить 200 рублей, а за квартплату отдать 100, то вместе счет за коммунальные платежи -200+(-100) = -300 р.

Применение в науках

После того, как стало понятно, что такое целое число в математике, можно разобраться с его применением. А используют этот тип чисел в разных сферах:

• прикладные науки;
• информатика;
• общая алгебра.

При исследованиях различных объектов природы некоторые данные записываются отрицательными и положительными числами. Это удобно в том случае, если приходится составлять таблицы для финансовых отчетов, формировать задачи с неделимыми предметами — временными периодами, единицами техники, живыми объектами.

В физике для описания микромира используются маленькие квантовые числа, все они являются целыми или полуцелыми. А для решения задач с ними разработаны специальные математические методы: теория диофантовых уравнений или целочисленное программирование.

Информатика также оперирует целыми числами. В этой сфере они используются как один из видов данных в языках программирования. Они превращаются в фиксированный набор битов, один из них кодирует знак, а другой сами цифры. У современных компьютеров есть большой набор команд для операций с целочисленными выражениями. В общей алгебре выстроена четкая иерархия множеств. Натуральные числа входят в целые, которые включены в рациональные. Также есть вещественные и иррациональные выражения.

Множества чисел бесконечны. Целых столько же, сколько и натуральных. На них похожи некоторые алгебраические структуры: гауссовы комплексные и формулы Эйзенштейна. С целыми значениями можно выполнять любые арифметические действия, осуществлять проверки и описывать изменения величин.