Содержание
Содержание
Поточечная сходимость [ править ]
То, как была определена сумма функционального ряда, не учитывает то, что функция — закон соответствия, который каждому [math]x in E[/math] сопоставляет некоторое число. При этом, все [math]x[/math] фигурировали изолированно.
Пусть на [math]E[/math] [math]f_n[/math] обладает свойством [math]P[/math] (например, непрерывность на [math]E[/math] ). И пусть для любого [math] x in E [/math] есть предел соответствующей числовой последовательности. Возникает вопрос: "Будет ли [math]f = limlimits_
Приведем пример, показывающий, что если требовать лишь поточечной сходимости, то для [math] f [/math] свойство [math]P[/math] может отсутствовать.
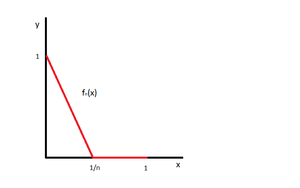
Все [math]f_n[/math] непрерывны на [math][0; 1][/math] . [math]f_n(0) = 1 o 1[/math] , [math]f(0) = 1[/math] .
[math]0 lt x leq 1[/math] : [math]frac1n o 0[/math] . Тогда, начиная с некоторого [math]N[/math] , все [math]frac1N lt x Rightarrow f_n(x) = 0[/math]Тогда [math]f[/math] будет разрывна в нуле, свойство непрерывности не сохранилось.
Равномерная сходимость [ править ]
Возникает вопрос: "Что ещё надо потребовать от поточечной сходимости, чтобы в пределе [math]P[/math] сохранилось?"
Классическое требование: равномерная сходимость.
| Определение: |
| [math]f_1, f_2, ldots[/math] равномерно сходится к [math]f(x)[/math] , если |
Пишут, что [math]f_n
ightrightarrows f[/math] .
| Определение: |
| Пусть на [math]E[/math] задан функциональный ряд [math]sumlimits_ |
Далее всё будем писать на языке функциональных рядов, так как их наиболее удобно использовать в математическом анализе, и вообще это очень круто и популярно.
Критерий Коши равномерной сходимости [ править ]
| Теорема (Критерий Коши равномерной сходимости): |
| Доказательство: |
| [math] riangleright[/math] |
|
[math]Longrightarrow[/math] Пусть ряд равномерно сходится.
[math]sumlimits_ ight| = |(S_m — S) + (S — S_ ight| leq |S_m — S| + |S_ По определению равномерной сходимости, [math]forall varepsilon exists N forall p gt N forall x in E : |S_p(x) — S(x)| lt varepsilon[/math] . [math]m, n — 1 gt N [/math]В силу предыдущего неравенства, [math]forall x in E : left|sumlimits_ По условию критерия Коши, [math]forall m geq n gt N forall x in E : left|sumlimits_ Как и в первой половине доказательства, [math]|S_m(x) — S_ Значит, определение равномерной сходимости проверено. |
| [math] riangleleft[/math] |
Признак Вейерштрасса [ править ]
Существует простой признак для проверки равномерной сходимости (признак Вейерштрасса)
Можно рассматривать [math]sumlimits_
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.
| Теорема (Вейерштрасс): |
Применим критерий Коши:
[math]left|sumlimits_ight|[/math] [math]leq sumlimits_
Сопоставляя с предыдущим неравенством, которое верно [math]forall x[/math] ,
[math]left|sumlimits_ight| lt varepsilon[/math] . Тогда, по критерию Коши, ряд равномерно сходится.
Признак Абеля-Дирихле [ править ]
| Теорема (Абель-Дирихле): |
| Доказательство: |
| [math] riangleright[/math] |
|
Монотонность последовательности [math]b_n(x)[/math] позволяет при каждом [math]x in E[/math] записать оценку: [math] |sumlimits_где [math] n — 1 leq k leq m [/math] и в качестве [math] A_k(x)[/math] возьмем [math] S_k(x) — S_(x) [/math] . Приводимые ниже признаки являются аналогами признаков Абеля и Дирихле для случая числовых рядов. Напомним сначала следующее утверждение. Т ЕОРЕМА 5. Предположим, что n , < a k >n k = 1 — монотонная число- вая последовательность, < b k >n k = 1 — произвольная числовая последовательность. Тогда имеет место оценка ≤ (| a 1 | + 2 | a n |) max ∑ b i . Указанное в теореме неравенство называется неравенством Абеля. Т ЕОРЕМА 6 ( ПРИЗНАК Д ИРИХЛЕ ). Предположим, что для функцио- нального ряда ∑ a n ( x ) b n ( x ) , x I выполняются следующие условия: 1) для каждого x I числовая последовательность < a n ( x )>n +∞ = 1 явля- 2) a n ( x ) 0 на промежутке I ; 3) существует такая константа M , что для всех n ≥ 1 , x I имеет Тогда ряд ∑ a n ( x ) b n ( x ) равномерно сходится на промежутке I . Для произвольных натуральных n , p и любого x I из условия 3) теоремы получаем: ∑ b k ( x ) − ∑ b k ( x ) Воспользуемся условием 2) формулировки теоремы. Выберем произвольное ε > 0 и найдем такое N , что при n ≥ N для всех x I выполняется неравенство | a n ( x ) | ε . Применяя для произвольного фиксированного x I неравенство Абеля к числовым последовательностям < a k ( x )>n k + = n p + 1 и < b k ( x )>n k + = n p + 1 ,
a k ( x ) b k ( x ) ≤ (| a n + 1 ( x ) | + 2 | a n + p ( x ) |) max ∑ a k ( x ) b k ( x ) ≤ 6 ε M . 1 ≤ q ≤ p k = n + 1 В силу произвольности ε , из критерия Коши равномерной сходимости функционального ряда выводим равномерную сходимость ряда З АМЕЧАНИЕ . Условие 2) формулировки теоремы может быть пере- формулировано так: частичные суммы ряда ∑ b n ( x ) равномерно ограни- чены на промежутке I . С ЛЕДСТВИЕ ПРИЗНАКА Д ИРИХЛЕ . Предположим, что последовательность функций < a n >+∞ n = 1 , определенных на промежутке I , удовлетворяет следующим условиям: 1) для любого x I числовая последовательность < a n ( x )>n +∞ = 1 являет- 2) a n ( x ) 0 на промежутке I . Тогда функциональный ряд ∑ ( − 1) n − 1 a n ( x ) равномерно сходится на про- Это утверждение вытекает из признака Дирихле, если положить b n ( x ) = ( − 1) n − 1 , n , x I . Отметим, что приведенное следствие является аналогом (для случая функциональных рядов) признака Лейбница сходимости числового ряда. П РИМЕР . Доказать равномерную сходимость ряда ∑ промежутке 0 ≤ x ≤ 1 при любом α > 0 . Р ЕШЕНИЕ . Полагаем b ( x ) = ( − 1) n − 1 x n , При любом фиксированном x [0,1] последовательность < a n ( x )>n +∞ = 1 является убывающей. Из оценки вытекает, что a n ( x ) 0 на промежутке [0,1] .
Частичные суммы ряда ∑ b n ( x ) имеют вид S n ( x ) = ∑ b k ( x ) = ∑ ( − 1) k − 1 x k = Оценивая модуль числителя последней дроби сверху, а знаменатель снизу, получаем: | x − ( − 1) n x | ≤ | x | + | ( − 1) n x | ≤ 2, 1 + x ≥ 1. Отсюда следует, что для любого x [0,1] имеет место неравенство | S n ( x ) | ≤ 2. Все условия признака Дирихле выполнены, следовательно, рассматриваемый ряд сходится на промежутке [0,1] равномерно. Отметим в заключение, что при α > 1 равномерная сходимость рассматриваемого ряда может быть выведена из признака Вейерштрасса. Действительно, для любого x [0,1] выполняется оценка |




