Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).
Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.
Рис. 3.16. Граф для примера 82
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.
С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Определение
Эксцентриситетом вершины называется расстояние до самой дальней вершины графа.
Радиусом графа называется минимальный эксцентриситет среди всех вершин графа
Диаметром графа — это наибольшее расстояние между всеми парами вершин графа
Центральной вершиной графа является вершина чей эксцентриситет равен радиусу графа.
Периферийной вершиной графа является вершина чей эксцентриситет равен диаметру графа.
Поиск радиуса и диаметра
Сервис граф онлайн позволит вам найти радиус и диаметр, а также укажет центральные и периферийные вершины. Для этого выберете пункт меню Алгоритмы -> Поиск радиуса и диаметра графа.
© Граф Online — создание и визуализация графа в два клика или по матрице смежности и поиск кратчайшего пути, поиск компоненты связности, поиск Эйлеровго цикла. Поделиться: Twitter, Facebook, В Контакте. 2016. (Edit — History — Print — Recent Changes — Search)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3615 |
| 2 | wxhtxdy | 3520 |
| 3 | Radewoosh | 3414 |
| 4 | Benq | 3368 |
| 5 | sunset | 3351 |
| 6 | mnbvmar | 3287 |
| 7 | LHiC | 3276 |
| 8 | ecnerwala | 3230 |
| 9 | stO | 3203 |
| 10 | TLE | 3145 |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | Errichto | 189 |
| 2 | Radewoosh | 176 |
| 3 | tourist | 173 |
| 4 | antontrygubO_o | 172 |
| 5 | PikMike | 167 |
| 6 | Vovuh | 166 |
| 7 | majk | 161 |
| 8 | rng_58 | 156 |
| 9 | Um_nik | 155 |
| 10 | 300iq | 154 |
Блог пользователя Bekzhan.Kassenov
Центр графа и его нахождение
Время от времени на CodeForces появляются вопросы о центре, радиусе и диаметре графа (смог нагуглить только о дереве, хотя было больше). В этом топике даны определения этим понятиям а также описаны алгоритмы для их нахождения.
Задача: дан не взвешенный неориентированный граф G = (V, E) , где V это множество вершин, а E — множество ребер. Необходимо найти его радиус, диаметр и центр.
Определим d i, j как кратчайшее расстояние между парой вершин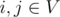 
. Тогда диаметр графа определяется как максимально возможное среди всех кратчайших расстояний между парой вершин:
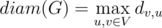
Также введем понятие эксцентриситета вершины как максимальное расстояние от вершины до какой-либо другой:
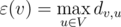
Зная эксцентриситет всех вершин, можно определить и радиус графа, как минимальный из них:
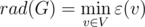
Сразу можно заметить, что диаметр графа это максимальный эксцентриситет в графе, т.е:
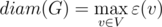
Центром графа назовем все вершины с эксцентриситетом, равным радиусу графа:
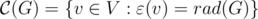
Определения даны и в голову приходит тривиальный алгоритм для нахождения центра, радиуса и диаметра для произвольного графа при помощи алгоритма Флойда-Уоршелла:
Теперь немного изменим постановку задачи: допустим, что граф G является деревом. Для дерева несложно доказать следующий факт: количество вершин в центре дерева равно одному или двум.
На CodeForces когда-то слышал следующий алгоритм для нахождения центра дерева: с помощью BFS-а из любой вершины (обозначим ее как v1 ) найти самую удаленную от v1 вершину (обозначим как v2 ), затем запустить BFS из v2 , выбрать любую самую удаленную от v2 вершину (пусть будет v3 ). Вершина(-ы) на середине пути между v2 и v3 образуют центр графа, расстояние между ними — диаметр. Радиусом же будет половина диаметра, округленная вверх: (diam(G) + 1) / 2 . Реализацию этого алгоритма здесь приводить не буду, так как она мне показалась несколько громоздкой. Вместо этого приведу другой алгоритм, который мне показался проще в реализации.
Теорема: Пусть L — множество всех листьев графа. Если |V| ≤ 2 , то L является центром графа, иначе можно удалить все листья и центр графа не изменится:
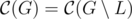
Эта теорема приводит нас к следующему алгоритму: будем удалять листья дерева, слой за слоем, пока не останется ≤ 2 вершин. Эти вершины и будут центром графа. Реализация данного алгоритма очень похожа на поиск в ширину:
Нетрудно доказать, что после исполнения данного алгоритма, центр дерева будет во множестве c ,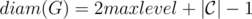 
и rad(G) = (diam(G) + 1) / 2 .
Задачек на порешать сходу не нашел, так что если знаете — ждем в комментах.
Задачки по теме:
Спасибо за внимание, насчет опечаток просьба писать в личку.
Загрузка...
