В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
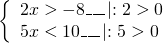— 8\_\_\_left| <:2 >0>
ight.\ 5x 0>
ight. end
ight.]" title="Rendered by QuickLaTeX.com"/>
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
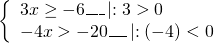0>
ight.\ — 4x > — 20\_\_\_left| <:( - 4)
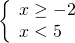
Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
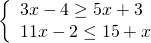
Переносим неизвестные в одну сторону, известные — в другую:
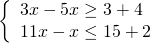
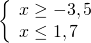
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
4) Сколько целых чисел являются решениями системы неравенств?
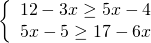
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:
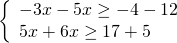
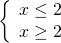
Решение неравенств отмечаем на числовых прямых.
Множество решений системы состоит из единственного элемента — <2>. 2 — целое число, следовательно, решением данной системы является одно целое число.
kor.giorgio@gmail.com Выход
Программа для решения линейных, квадратных и дробных неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Причём, если в процессе решения одного из неравенств нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).
Данная программа может быть полезна учащимся старших классов при подготовке к контрольным работам, родителям для контроля решения неравенств их детьми.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5y +1/7y^2
Результат: ( 3frac<1> <3>— 5frac<6> <5>y + frac<1><7>y^2 )
При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)
Выберите нужный знак неравенства и введите многочлены в поля ниже.
Готовимся к экзамену по математике за период обучения на II ступени общего среднего образования
13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:
>
Загрузка...
