Производная от константы равна нулю

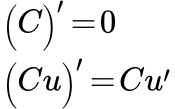
Правила дифференцирования функций, содержащих постоянные

Здесь мы рассмотрим следующие правила, связанные с дифференцированием функций, содержащих постоянные:
(1) ;
(2) ,
где C – постоянная, u – дифференцируемая функция от независимой переменной :
.

Вначале мы докажем эти правила. Затем приведем примеры вычисления производных.

Производная постоянной функции

Выясним, чему равна производная постоянной функции. Для этого применим определение производной:
(3) .
Пусть функция является постоянной, которую обозначим как :
.
То есть не зависит от x . Значения переменной y одинаковы при любых значениях переменной x и равны . Тогда
;
;
.
То есть производная постоянной функции равна нулю:
.

Вынесение постоянной за знак производной

Теперь докажем правило (2). То есть если является дифференцируемой функцией от переменной x (на некотором множестве ее значений), то при дифференцировании, постоянный множитель можно выносить за знак производной:
(2) .

Доказательство

Поскольку является дифференцируемой функцией, то существует производная этой функции:
.

Рассмотрим функцию от независимой переменной x следующего вида:
.
По определению производной

.

То есть
.
Что и требовалось доказать.

Примеры

Проиллюстрируем применение рассмотренных правил (1) и (2) на примерах.

Пример 1

Найти производную функции
.

Функция не содержит переменную x . Поэтому она является постоянной. Поскольку производная постоянной функции равна нулю, то производная заданной функции равна нулю:
.

Пример 2

Найти производную функции от переменной x :
.

Здесь является постоянной. Выносим ее за скобки и используем таблицу производных:
.

Пример 3

Применим свойство логарифма
.
Тогда
.
Выносим постоянную 6 за скобки и применяем таблицу производных:
.

Пример 4

Продифференцировать функцию от переменной x :
.

Применим свойство экспоненты
.
Тогда
.
Но является постоянной, не зависящей от переменной величиной. Выносим ее за скобки и используем таблицу производных:
.

Пример 5

Продифференцировать по переменной x функцию, состоящую из корней:
.

Выносим постоянную за скобки и применяем правило дифференцирования степенной функции из таблицы производных:
.
Тогда
.
Приведем корни к одинаковой степени и упростим результат:
.

Автор: Олег Одинцов . Опубликовано: 14-10-2016

Приведем сводную таблицу для удобства и наглядности при изучении темы.

Константа y = C

Степенная функция y = x p

( x p ) ‘ = p · x p — 1

Показательная функция y = a x

( a x ) ‘ = a x · ln a

В частности, при a = e имеем y = e x

Логарифмическая функция

( log a x ) ‘ = 1 x · ln a

В частности, при a = e имеем y = ln x

Тригонометрические функции

( sin x ) ‘ = cos x ( cos x ) ‘ = — sin x ( t g x ) ‘ = 1 cos 2 x ( c t g x ) ‘ = — 1 sin 2 x

Обратные тригонометрические функции

( a r c sin x ) ‘ = 1 1 — x 2 ( a r c cos x ) ‘ = — 1 1 — x 2 ( a r c t g x ) ‘ = 1 1 + x 2 ( a r c c t g x ) ‘ = — 1 1 + x 2

Гиперболические функции

( s h x ) ‘ = c h x ( c h x ) ‘ = s h x ( t h x ) ‘ = 1 c h 2 x ( c t h x ) ‘ = — 1 s h 2 x

Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.

Производная постоянной

Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x 0 = x , где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f ( x ) = C . Составим запись предела отношения приращения функции к приращению аргумента при ∆ x → 0 :

lim ∆ x → 0 ∆ f ( x ) ∆ x = lim ∆ x → 0 C — C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Обратите внимание, что под знак предела попадает выражение 0 ∆ x . Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.

Итак, производная постоянной функции f ( x ) = C равна нулю на всей области определения.

Даны постоянные функции:

f 1 ( x ) = 3 , f 2 ( x ) = a , a ∈ R , f 3 ( x ) = 4 . 13 7 22 , f 4 ( x ) = 0 , f 5 ( x ) = — 8 7

Необходимо найти их производные.

Решение

Опишем заданные условия. В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а — любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби — 8 7 .

Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)

f 1 ‘ ( x ) = ( 3 ) ‘ = 0 , f 2 ‘ ( x ) = ( a ) ‘ = 0 , a ∈ R , f 3 ‘ ( x ) = 4 . 13 7 22 ‘ = 0 , f 4 ‘ ( x ) = 0 ‘ = 0 , f 5 ‘ ( x ) = — 8 7 ‘ = 0

Производная степенной функции

Переходим к степенной функции и формуле ее производной, имеющей вид: ( x p ) ‘ = p · x p — 1 , где показатель степени p является любым действительным числом.

Приведем доказательство формулы, когда показатель степени – натуральное число: p = 1 , 2 , 3 , …

Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:

( x p ) ‘ = lim ∆ x → 0 = ∆ ( x p ) ∆ x = lim ∆ x → 0 ( x + ∆ x ) p — x p ∆ x

Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:

( x + ∆ x ) p — x p = C p 0 + x p + C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · ( ∆ x ) 2 + . . . + + C p p — 1 · x · ( ∆ x ) p — 1 + C p p · ( ∆ x ) p — x p = = C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · ( ∆ x ) 2 + . . . + C p p — 1 · x · ( ∆ x ) p — 1 + C p p · ( ∆ x ) p

( x p ) ‘ = lim ∆ x → 0 ∆ ( x p ) ∆ x = lim ∆ x → 0 ( x + ∆ x ) p — x p ∆ x = = lim ∆ x → 0 ( C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · ( ∆ x ) 2 + . . . + C p p — 1 · x · ( ∆ x ) p — 1 + C p p · ( ∆ x ) p ) ∆ x = = lim ∆ x → 0 ( C p 1 · x p — 1 + C p 2 · x p — 2 · ∆ x + . . . + C p p — 1 · x · ( ∆ x ) p — 2 + C p p · ( ∆ x ) p — 1 ) = = C p 1 · x p — 1 + 0 + 0 + . . . + 0 = p ! 1 ! · ( p — 1 ) ! · x p — 1 = p · x p — 1

Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.

Чтобы привести доказательство для случая, когда p — любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.

Рассмотрим два случая: когда x положительны и когда x отрицательны.

Итак, x > 0 . Тогда: x p > 0 . Логарифмируем равенство y = x p по основанию e и применим свойство логарифма:

y = x p ln y = ln x p ln y = p · ln x

На данном этапе получили неявно заданную функцию. Определим ее производную:

( ln y ) ‘ = ( p · ln x ) 1 y · y ‘ = p · 1 x ⇒ y ‘ = p · y x = p · x p x = p · x p — 1

Теперь рассматриваем случай, когда x – отрицательное число.

Если показатель p есть четное число, то степенная функция определяется и при x 0 , причем является четной: y ( x ) = — y ( ( — x ) p ) ‘ = — p · ( — x ) p — 1 · ( — x ) ‘ = = p · ( — x ) p — 1 = p · x p — 1

Тогда x p 0 и возможно составить доказательство, используя логарифмическую производную.

Если p есть нечетное число, тогда степенная функция определена и при x 0 , причем является нечетной: y ( x ) = — y ( — x ) = — ( — x ) p . Тогда x p 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y ‘ ( x ) = ( — ( — x ) p ) ‘ = — ( ( — x ) p ) ‘ = — p · ( — x ) p — 1 · ( — x ) ‘ = = p · ( — x ) p — 1 = p · x p — 1

Последний переход возможен в силу того, что если p — нечетное число, то p — 1 либо четное число, либо нуль (при p = 1 ), поэтому, при отрицательных x верно равенство ( — x ) p — 1 = x p — 1 .

Итак, мы доказали формулу производной степенной функции при любом действительном p .

f 1 ( x ) = 1 x 2 3 , f 2 ( x ) = x 2 — 1 4 , f 3 ( x ) = 1 x log 7 12

Определите их производные.

Решение

Часть заданных функций преобразуем в табличный вид y = x p , опираясь на свойства степени, а затем используем формулу:

f 1 ( x ) = 1 x 2 3 = x — 2 3 ⇒ f 1 ‘ ( x ) = — 2 3 · x — 2 3 — 1 = — 2 3 · x — 5 3 f 2 ‘ ( x ) = x 2 — 1 4 = 2 — 1 4 · x 2 — 1 4 — 1 = 2 — 1 4 · x 2 — 5 4 f 3 ( x ) = 1 x log 7 12 = x — log 7 12 ⇒ f 3 ‘ ( x ) = — log 7 12 · x — log 7 12 — 1 = — log 7 12 · x — log 7 12 — log 7 7 = — log 7 12 · x — log 7 84

Производная показательной функции

Выведем формулу производной, взяв за основу определение:

( a x ) ‘ = lim ∆ x → 0 a x + ∆ x — a x ∆ x = lim ∆ x → 0 a x ( a ∆ x — 1 ) ∆ x = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = " open=" 0 0

Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z = a ∆ x — 1 ( z → 0 при ∆ x → 0 ). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a ( z + 1 ) = ln ( z + 1 ) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.

Осуществим подстановку в исходный предел:

( a x ) ‘ = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln ( z + 1 ) = = a x · ln a · lim ∆ x → 0 1 ln ( z + 1 ) 1 z = a x · ln a · 1 ln lim ∆ x → 0 ( z + 1 ) 1 z

Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:

( a x ) ‘ = a x · ln a · 1 ln lim z → 0 ( z + 1 ) 1 z = a x · ln a · 1 ln e = a x · ln a

Даны показательные функции:

f 1 ( x ) = 2 3 x , f 2 ( x ) = 5 3 x , f 3 ( x ) = 1 ( e ) x

Необходимо найти их производные.

Решение

Используем формулу производной показательной функции и свойства логарифма:

f 1 ‘ ( x ) = 2 3 x ‘ = 2 3 x · ln 2 3 = 2 3 x · ( ln 2 — ln 3 ) f 2 ‘ ( x ) = 5 3 x ‘ = 5 3 x · ln 5 1 3 = 1 3 · 5 3 x · ln 5 f 3 ‘ ( x ) = 1 ( e ) x ‘ = 1 e x ‘ = 1 e x · ln 1 e = 1 e x · ln e — 1 = — 1 e x

Производная логарифмической функции

Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:

( log a x ) ‘ = lim ∆ x → 0 log a ( x + ∆ x ) — log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x · log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a

Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim ∆ x → 0 1 + ∆ x x x ∆ x = e является верным в соответствии со вторым замечательным пределом.

Заданы логарифмические функции:

f 1 ( x ) = log ln 3 x , f 2 ( x ) = ln x

Необходимо вычислить их производные.

Решение

Применим выведенную формулу:

f 1 ‘ ( x ) = ( log ln 3 x ) ‘ = 1 x · ln ( ln 3 ) ; f 2 ‘ ( x ) = ( ln x ) ‘ = 1 x · ln e = 1 x

Итак, производная натурального логарифма есть единица, деленная на x .

Производные тригонометрических функций

Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.

Согласно определению производной функции синуса, получим:

( sin x ) ‘ = lim ∆ x → 0 sin ( x + ∆ x ) — sin x ∆ x

Формула разности синусов позволит нам произвести следующие действия:

( sin x ) ‘ = lim ∆ x → 0 sin ( x + ∆ x ) — sin x ∆ x = = lim ∆ x → 0 2 · sin x + ∆ x — x 2 · cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Наконец, используем первый замечательный предел:

sin ‘ x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Итак, производной функции sin x будет cos x .

Совершенно также докажем формулу производной косинуса:

cos ‘ x = lim ∆ x → 0 cos ( x + ∆ x ) — cos x ∆ x = = lim ∆ x → 0 — 2 · sin x + ∆ x — x 2 · sin x + ∆ x + x 2 ∆ x = = — lim ∆ x → 0 sin ∆ x 2 · sin x + ∆ x 2 ∆ x 2 = = — sin x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = — sin x

Т.е. производной функции cos x будет – sin x .

Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:

t g ‘ x = sin x cos x ‘ = sin ‘ x · cos x — sin x · cos ‘ x cos 2 x = = cos x · cos x — sin x · ( — sin x ) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g ‘ x = cos x sin x ‘ = cos ‘ x · sin x — cos x · sin ‘ x sin 2 x = = — sin x · sin x — cos x · cos x sin 2 x = — sin 2 x + cos 2 x sin 2 x = — 1 sin 2 x

Производные обратных тригонометрических функций

Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.

Производные гиперболических функций

Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:

s h ‘ x = e x — e — x 2 ‘ = 1 2 e x ‘ — e — x ‘ = = 1 2 e x — — e — x = e x + e — x 2 = c h x c h ‘ x = e x + e — x 2 ‘ = 1 2 e x ‘ + e — x ‘ = = 1 2 e x + — e — x = e x — e — x 2 = s h x t h ‘ x = s h x c h x ‘ = s h ‘ x · c h x — s h x · c h ‘ x c h 2 x = c h 2 x — s h 2 x c h 2 x = 1 c h 2 x c t h ‘ x = c h x s h x ‘ = c h ‘ x · s h x — c h x · s h ‘ x s h 2 x = s h 2 x — c h 2 x s h 2 x = — 1 s h 2 x

Рекомендуется выучить формулы из таблицы производных: они не столь сложны для запоминания, но экономят много времени, когда необходимо решать задачи дифференцирования.

Вычисляет производную заданной функции.

Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.

Калькулятор производных

Производная функции

Синтаксис описания формул

В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, — — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.