Ряды лорана примеры решения

Пример 1. Требуется получить все возможные разложения в ряд Лорана по степеням z – 2 функции .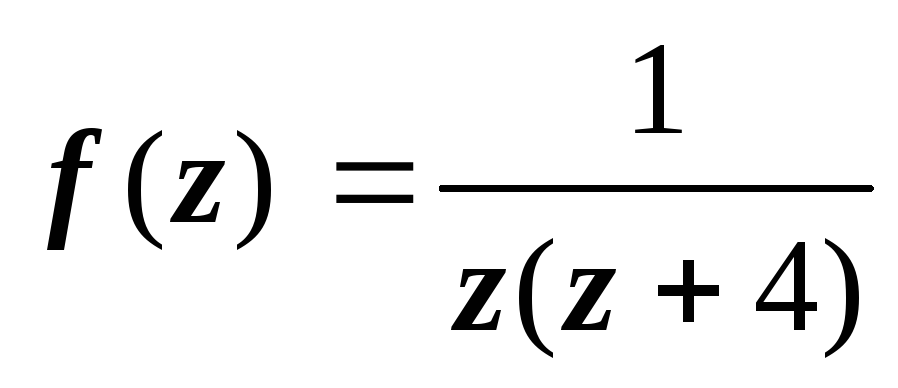

Здесь z = 2; функция теряет аналитичность в точках

z₁ = 0, z₂ = -4. Легко видеть, что существует три области аналитичности с центром в z (один круг и два кольца), на границах которых функция теряет аналитичность:

1. | z – 2| 6. В каждой из этих областей разложение будет таким:

1. В первой области (круге) функция аналитична, поэтому ряд Лорана будет совпадать с рядом Тейлора. 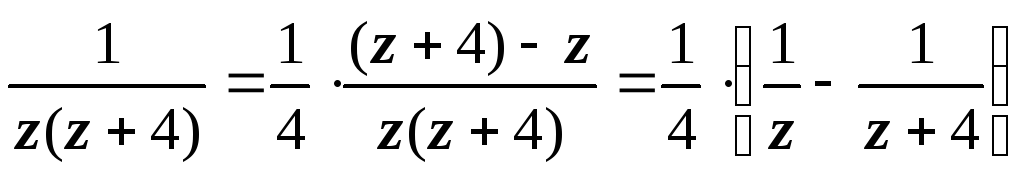— таково разложение f(z) на простые дроби, разлагаем в ряд Тейлора каждую их них. 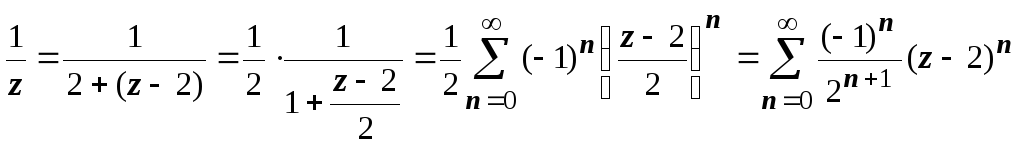, где | z – 2| 4. 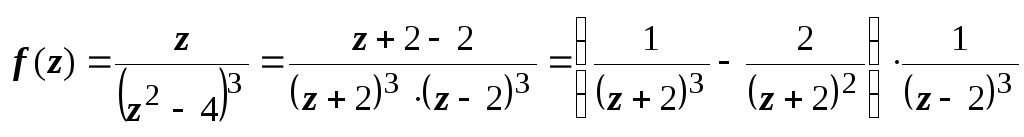. Первый множитель уже представлен в виде суммы по степеням | z + 2|, работаем со вторым. Третью степень в знаменателе получим, дважды дифференцируя разложение функции .

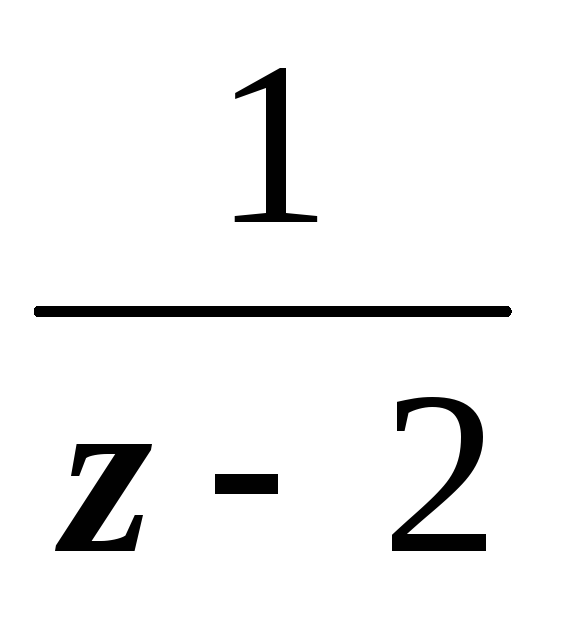1. В первом кольце 0 4 получаем ,,,.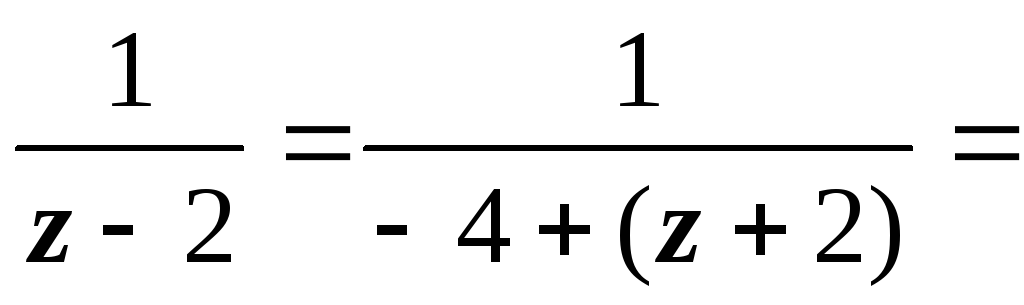

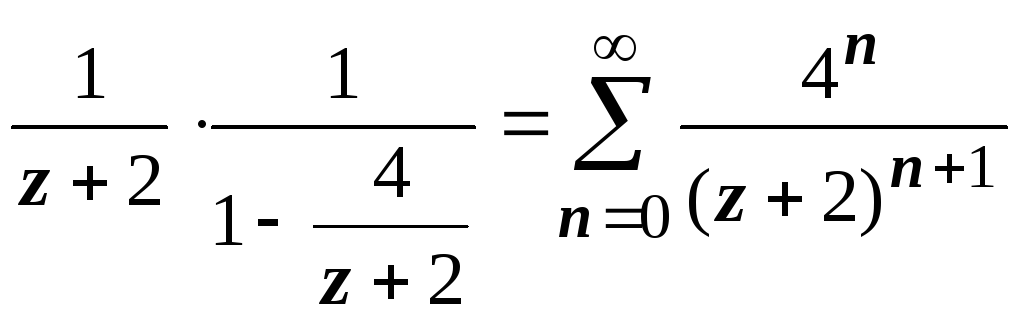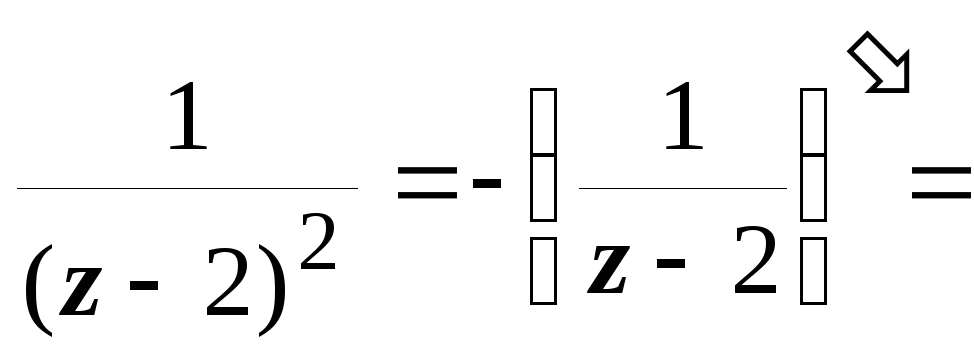
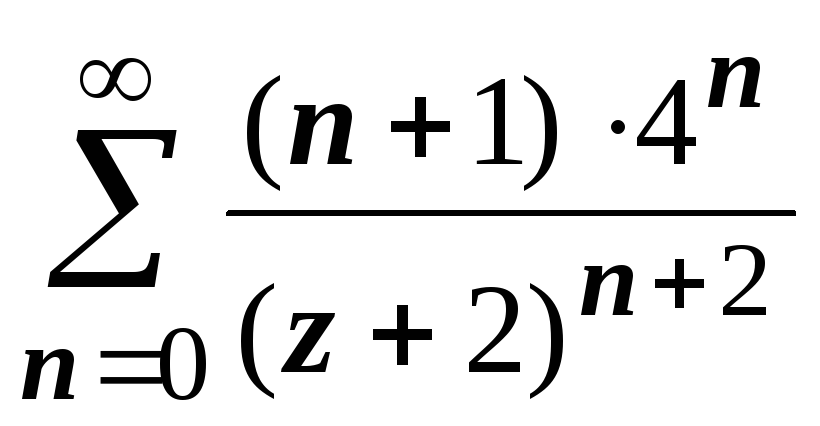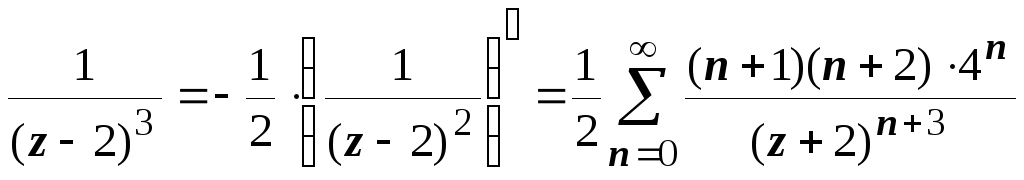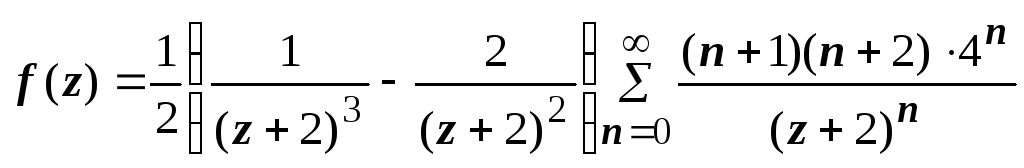Среди множества рядов, близких к степенным по своему строению и свойствам, являются ряды, расположенные по целым отрицательным степеням z – z:

Сделаем замену в (2.103), получим:

Как известно радиус сходимости полученного ряда есть число R (2.90): если R = 0, то ряд (2.104) сходится в точке t = 0; если 0 Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Страницы работы

Содержание работы

Тема 6-1. Ряды Тейлора и Лорана

Лекция 7

Введение

Пусть дана функция f(z), аналитическая в некоторой окрестности точки а.

Тогда в круге сходимости эта функция может быть представлена рядом Тейлора:

f(z)=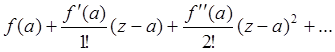

а само равенство называют разложением функции в ряд Тейлора.

Замечание: многоточие, которым заканчивается правая часть функции f(z), символизирует тот факт, что точное равенство достигается за счет бесконечного множества слагаемых. Поэтому последнего слагаемого нет.

Находим производные функции f(z) = z 5 : .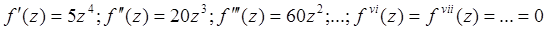

Определим значения производных в точке a = i: .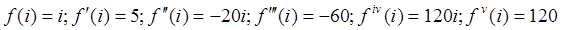

Отсюда 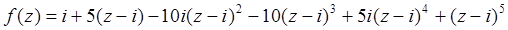— многочлен 5-ой степени.

Формула Тейлора

Если функция f(z) имеет в точке а производные до порядка n включительно, то ее можно представить формулой Тейлора порядка n:

f(z) =; .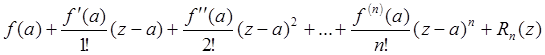

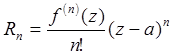Положив а = 0, можно разложить функцию f(z) в ряд Маклорена: f(z)=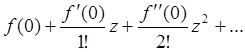

Показательная и тригонометрическая функция комплексного переменного

Разложим e z и e iz в ряд Маклорена:

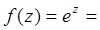
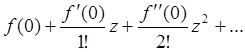
для e z для e iz

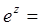
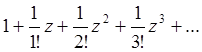
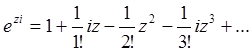
Применив разложение в ряд к функциям sinz и cosz, получим:

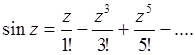
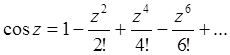
f (n) (z)=e z f (n) (0) =1

f (n) (z)=i n e zi f (n) (0) =1

Произведя замену z на iz для функции e z и разделив e iz на Ree iz и Ime iz части, легко увидеть, что e zi есть сумма cosz и i× sinz.

Cоотношения между функциями, выражаемые как:

; ;

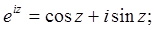
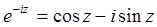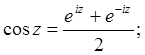
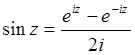называются формулами Эйлера.

Области сходимости рядов

Рассмотрим два ряда:

1. 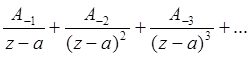, область сходимости которого определяется неравенством r .

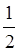2 – ой ряд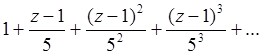

По формуле Даламбера радиус сходимости R = 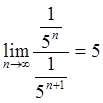и ряд сходится , если |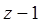| 2 -(1/3!)×cosp/4×(x-p/4) 3 +…=

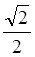=[1+(1/1!)×(x-p/4)-(1/2!)×(x-p/4) 2 -(1/3!)×(x-p/4) 3 +…].

2. Найти область сходимости ряда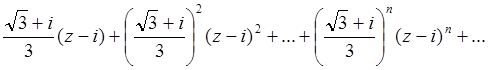

Решение: R=.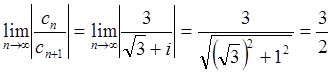

Областью сходимости ряда является круг |z – i| 5, и 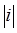= 1 Þ|z| n ® 0)

Тогда в окрестности точки z =0 выполняется неравенство |q|= 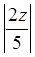2 + 32/t +24 +8t +t 2 =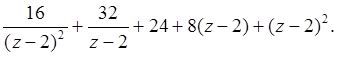

Главная часть содержит два члена, а правильная – три.

Так как разложение содержит конечное число членов, то оно справедливо для любой точки плоскости, кроме z =2.

Точка z =2 является полюсом второго порядка.

Вычетом этой функции относительно полюса z =2 является коэффициент А_-1 при (z – 2) -1 , т.е. 32.