Свойства символа о малое

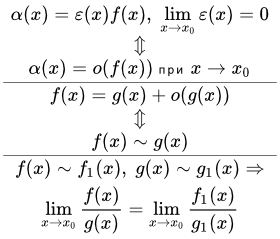
Определения

Определение о малого
Символом о малое обозначают любую бесконечно малую функцию o ( f ( x )) по сравнению с заданной функцией f ( x ) при аргументе, стремящемся к некоторому конечному или бесконечному числу x .

Функция α называется бесконечно малой по сравнению с функцией f при :
при
(читается: « есть о малое от при »),
если существует такая проколотая окрестность точки , на которой
при ,
где – бесконечно малая функция при :
.

Заметим, что просто бесконечно малая функция при является бесконечно малой по сравнению с постоянной функцией, не равной нулю.

Если, в предыдущем определении, f является бесконечно малой функцией при , то говорят, что является бесконечно малой более высокого порядка, чем f при .

Определение О большого
Символом О большое обозначают любую функцию , ограниченную относительно функции при аргументе, стремящемся к некоторому конечному или бесконечному числу x .

Функция f ограничена относительно функции g при x → x :
при
(читается: « есть О большое от при »),
если функции f и g определены на некоторой проколотой окрестности точки и существует такое число C , что на этой окрестности выполняется неравенство:
.

Просто ограниченная, на некоторой проколотой окрестности точки , функция является ограниченной по сравнению с постоянной функцией, не равной нулю.

Функции f и g называются функциями одного порядка при :
при ,
если и при .

Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.

Свойства и теоремы

Теорема. Свойства о малого
1) Если , то при .
2) Если на некоторой проколотой окрестности точки ,
и , то
.
3.1) , где c ≠ 0 – постоянная.
3.2) ;
3.3) .
Доказательство ⇓

Свойства о малого, применяемые в степенных рядах
Здесь m и n – натуральные числа, .
;
;
, если ;
;
;
;
, где ;
, где c ≠ 0 – постоянная;
.

Для доказательства этих свойств нужно выразить о малое через бесконечно малую функцию:
, где .

Свойства эквивалентных функций
1) Свойство симметрии. Если, при , , то .
2) Свойство транзитивности. Если, при , и , то .
3) Если , то при .
Доказательство ⇓

Теорема о связи эквивалентных функций с о малым
Для того чтобы две функции и были эквивалентными (или асимптотически равными), необходимо и достаточно чтобы при выполнялось условие:
.
Доказательство ⇓

Это свойство часто записывают так:
.
При этом говорят, что является главной частью при . При этом главная часть определена не однозначно. Любая эквивалентная функция является главной частью к исходной.
В силу свойства симметрии:
.

Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство ⇓

В силу свойства симметрии эквивалентных функций, если не существует один из этих пределов, то не существует и другой.

Поскольку любая функция, определенная на некоторой проколотой окрестности точки , эквивалентна самой себе, то существуют пределы
.

Заменив функции g и g ₁ на 1/ g и 1/ g ₁ , получим аналогичную теорему для произведения.
Если, при , и , то
.
Это означает, что если существует один предел, то существует и другой. Если не существует один из этих пределов, то не существует и второй.

Лемма. Признак функций одного порядка
Если существует конечный ненулевой предел
(Л1.1) ,
то функции f и g одного порядка при :
при .
Доказательство ⇓

Доказательство свойств и теорем

Теорема. Свойства о малого

Пусть . Это означает, что существует такая проколотая окрестность точки , на которой определено отношение и поэтому . Тогда на этой окрестности
,
где . По условию
.
Тогда .
Свойство 1) доказано.

2) Если на некоторой проколотой окрестности точки ,
и , то
.

Поскольку , то на рассматриваемой проколотой окрестности точки ,
.
Поскольку , то
.
Свойство 2) доказано.

3.1) , где c ≠ 0 – постоянная.
3.2) ;
3.3) .

3.1). Пусть . Согласно определению о малого,
,
где . Введем функцию . Тогда
.
Поскольку , то
.
Свойство 3.1) доказано.

3.2). Докажем, что .
Пусть . Согласно определению о малого,
,
где .
Тогда ,
где . Поскольку
, то
.
Свойство 3.2) доказано.

3.3). Докажем, что .
Пусть . Согласно определению о малого,
,
где ,
.
Согласно арифметическим свойствам предела функции,
.
Тогда .
Свойство 3.3) доказано.

Эквивалентные функции

Свойства эквивалентных функций

Все формулировки ⇑ 1) Свойство симметрии. Если, при , , то .

Поскольку при , , то согласно определению эквивалентной функции, существует такая проколотая окрестность точки , на которой
,
где .
Поскольку функция имеет отличный от нуля предел, то по теореме об ограниченности снизу функции, имеющей ненулевой предел, существует такая проколотая окрестность точки , на которой . Поэтому на этой окрестности . Следовательно, на ней определена функция . Тогда
.
Согласно теореме о пределе частного двух функций,
.
Свойство доказано.

2) Свойство транзитивности. Если, при , и , то .

Теорема о связи эквивалентных функций с о малым

Все формулировки ⇑ Для того чтобы две функции и были эквивалентными (или асимптотически равными), необходимо и достаточно чтобы при выполнялось условие:
.

1. Необходимость. Пусть функции и являются эквивалентными при . Тогда
.
Поскольку , то
.
Тогда .
Необходимость доказана.

2. Достаточность. Пусть при ,
.
Тогда , где . Отсюда
.
Поскольку , то
.
Теорема доказана.

Теорема о замене функций эквивалентными в пределе частного

Все формулировки ⇑ Если, при , и и существует предел
, то существует и предел
.

Пусть, при , и . Тогда
, где
.
Поскольку существует предел , то существует такая проколотая окрестность точки , на которой функция определена и отлична от нуля. Поскольку , то, по теореме об ограниченности снизу функции, имеющей ненулевой предел, существует такая проколотая окрестность точки , на которой и, следовательно, . Тогда существует проколотая окрестность точки , на которой функция определена и отлична от нуля и, следовательно, определено частное :
.
Применяем арифметические свойства предела функции:
.

Признак функций одного порядка

Все формулировки ⇑ Лемма
Если существует конечный ненулевой предел
(Л1.1) ,
то функции f и g одного порядка при :
при .

Поскольку существует предел (Л1.1), то по теореме о пределе абсолютного значения функции, существует предел
.
Тогда согласно определению предела функции по Коши, для любого , существует такая проколотая окрестность точки , на которой
при .

Преобразуем неравенство и подставим :
;
;
(Л1.2) .
Из второго неравенства:
,
или .
Из первого неравенства (Л1.2):
,
или .

Использованная литература.
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов . Опубликовано: 15-04-2019 Изменено: 29-04-2019

Добрый день! Помогите, пожалуйста, разобраться в следующих формулах преобразования выражений, содержащих о-малое. $$f^(n-1)o(f)=o(f^n)$$ $$(o(f^n)/f)=o(f^(n-1))$$ Проблема в том, что я очень понимаю, как доказываются данные формулы. В частности, при $$x
ightharpoonup 0$$ справедливо $$x o(x^2)=o(x^3), x^2 o(x^3)=o(x^5)$$ Объясните, пожалуйста, чем обосновываются приведенные правила преобразования? Хочется понять, а не просто выучить формулы из методики. Спасибо.

задан 23 Дек ’18 11:30

1 ответ

В комментарий не уместилось из-за объёма.

Для упрощения можно считать, что величины не обращаются в ноль в некоторой (проколотой) окрестности. Тогда условие $%g=o(f)$% означает, что частное $%g/f$% бесконечно мало (стремится к нулю) при $%x o a$%. Тогда равенства типа $%xo(x^2)=o(x^3)$% становятся тривиальными: достаточно разделить обе части равенства на $%x^3$%.

В общем случае, если обращение в ноль возможно, и частное мы брать не можем, обозначение о-малого можно трактовать чуть иначе. А именно, считать, что $%g=o(f)$% означает $%g=fo(1)$%, где $%o(1)$% — бесконечно малая. Содержательно, это понимается так: $%g=o(f)$% выражает мысль, что $%g$% бесконечно мала по сравнению с $%f$%, то есть является произведением $%f$% на бесконечно малую величину.

Это вещи, которые вытекают прямо из определений (попутно можно заметить, что $%f=O(g)$% выражает мысль о том, что $%f$% равно произведению $%g$% на некоторую ограниченную величину). Использование О-символики подразумевает, что свойства мы один раз в самом начале проверяем (обосновываем), а потом используем уже автоматически. Из сказанного выше все упомянутые равенства тут же получаются: $%f^o(f)=f^fo(1)=f^o(1)=o(f^n)$%, и так далее.

В основе других равенств этого типа (наподобие $%o(f)+o(f)=o(f)$%) лежат известные факты вроде того, что сумма двух б.м. величин является бесконечно малой.

отвечен 23 Дек ’18 11:46

falcao
243k ● 1 ● 34 ● 48

Спасибо большое! Разрешите такой вопрос относительно равенства x o(x^2)=o(x^3). Я поняла, что для его доказательства достаточно разделить обе части на x^3. Но если провести рассуждения несколько иначе, то получается какая-то глупость. В частности, пусть f=x, g=o(x^2). По определению последняя запись означает что предел частного g/x^2 равен 0. Предел функции f=x равен 0 (поскольку x стремится к нулю). Тогда по теореме о пределе произведения, предел (x * g)/(x^2) равен нулю и, пользуясь определением o-малого, получаем, что xo(x^2)=xg=o(x^2). Подскажите, почему приведенные рассуждения неверны.

@Нина Аргентова: у Вас рассуждение верное в том смысле, что в нём нет ошибки как таковой. Да, конечно, при x->0 будет верно то, что xo(x^2)=o(x^2). Но это верно примерно в той же степени, как и рассуждение, что 2 меньше 10, 2 меньше 10, поэтому 2*2 меньше 100. Конечно, это правда, но это очень слабый факт. Вы никак не воспользовались тем, что первый множитель x=x^1 даёт вклад 1 в общий "порядок малости", который равен 1+2. Более прямая аналогия: вместо 1+2=3 доказано, что 1+2>=0+2=2.

«O» большое и «o» малое — математические обозначения для сравнения асимптотического поведения функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также при оценке сложности алгоритмов. В частности, фраза «сложность алгоритма есть O(n!)» означает, что при больших n время работы алгоритма (или общее количество операций) не более чем C · n!, где C — некая положительная константа (обычно в качестве параметра n берут объем входной информации алгоритма).

Определения

Пусть f(x) и g(x) — две функции, определенные в некоторой проколотой окрестности точки x, причем в этой окрестности g не обращается в ноль. Говорят, что:

• f является «O» большим от g при x → x, если существует такая положительная константа C, что для всех x из некоторой окрестности точки x имеет место неравенство

|f(x)|

• f является «о» малым от g при x → x, если для любой положительной константы c найдется такая окрестность точки x, что для всех x из этой окрестности имеет место неравенство

|f(x)|

Иначе говоря, в первом случае отношение |f|/|g| в окрестности точки x ограничено сверху, а во втором оно стремится к нулю.

Обозначение

«f является „O“ большим („о“ малым) от g»

Это обозначение очень удобно, но требует некоторой осторожности при использовании (а потому в наиболее элементарных учебниках его могут избегать). Дело в том, что это не равенство в обычном смысле, а несимметричное отношение

«если функция такова, как написано слева от знака равенства, то она и такова, как записано справа»:

в частности, можно писать

бессмысленны. Другой пример: при x → 0 верно, что

Вместо знака равенства методологически правильнее было бы употреблять знаки принадлежности и включения, понимая O( ) и o( ) как обозначения для множеств функций, то есть используя запись в форме

$ mathop O(x^2)subset o(x) $

Однако на практике такая запись встречается крайне редко, в основном в простейших случаях.

При использовании данных обозначений должно быть явно оговорено (или очевидно из контекста), о каких окрестностях (одно- или двусторонних; содержащих целые, вещественные или комплексные числа и т. п.) и о каких допустимых множествах функций идет речь (поскольку такие же обозначения употребляются и применительно к функциям многих переменных, к функциям комплексной переменной, к матрицам и др.).

Основные свойства

• o(f) = const × o(f); O(f) = const × O(f);
• o(f) = o(const × f); O(f) = O(const × f);
• o(f) = O(f);
• o(f) + o(f) = o(f); o(f) + O(f) = O(f); O(f) + O(f) = O(f);
• O(f) × O(g) = O(fg); o(f) × O(g) = o(fg); o(f) × o(g) = o(fg);
• O(O(f )) = O(f);
• o(o(f)), o(O(f)), O(o(f)) = o(f).

Примеры использования

• e x = 1 + x + x 2 /2 + O(x 3 ) при x → 0;
• n! = O((n/e) n+1/2 ) при $ n o infty $ .

Другие подобные обозначения

Реже используются обозначения:

• f = Ω(g) при x → x, если отношение |f(x)/g(x)| ограничено снизу положительной константой в некоторой окрестности точки x;
• f = Θ(g) при x → x, если отношение |f(x)/g(x)| ограничено положительными константами и сверху, и снизу, т. е. если одновременно f = O(g) и g = O(f).

История

Обозначение «„O“ большое» введено немецким математиком Паулем Бахманом (Paul Gustav Heinrich Bachmann) во втором томе его книги «Analytische Zahlentheorie» (Аналитическая теория чисел), вышедшем в 1894 году. Обозначение «„о“ малое» впервые использовано другим немецким математиком, Эдмундом Ландау (Edmund Georg Hermann Landau) в 1909 году; с работами последнего связана и популяризация обоих обозначений, в связи с чем их также называют символами Ландау.pl:Notacja dużego Osr:Велико О sv:Ordo th:สัญกรณ์โอใหญ่uk:Нотація Ландау